【力扣100题计划】课程表
题目链接:207. 课程表 - 力扣(LeetCode)
目录
题目描述:
前置知识:
拓扑排序基本概念:
算法实现 :
Kahn 算法(基于入度)
DFS 算法
思路分析:
问题抽象:有向图的拓扑排序问题
代码的实现思路:(基于入度)
具体代码实现:
复杂度分析:
题目描述:

前置知识:
拓扑排序基本概念:
拓扑排序(Topological Sorting)是针对有向无环图(DAG)的一种线性排序算法,它使得对于图中的每一条有向边
(u, v),u在排序中总是位于v的前面。拓扑排序常用于解决依赖关系问题,比如课程安排、任务调度等。
算法实现 :
Kahn 算法(基于入度)
计算入度:统计每个节点的入度(即有多少边指向它)。
初始化队列:将所有入度为 0 的节点加入队列。
拓扑排序:
从队列中取出一个节点
u,加入排序结果。遍历
u的所有邻居v,将v的入度减 1。如果
v的入度变为 0,则将v加入队列。终止条件:
如果排序结果包含所有节点,则拓扑排序成功。
否则,说明图中存在环,无法进行拓扑排序。
DFS 算法
递归访问:对每个未访问的节点进行 DFS。
标记访问状态:
visited[u] = false:未访问。
visited[u] = true:已访问但未完成(用于检测环)。
finished[u] = true:已完成(加入排序结果)。检测环:如果在 DFS 过程中遇到
visited[v] = true但finished[v] = false,则说明存在环。逆序加入结果:在 DFS 完成后,将节点逆序加入排序结果。
思路分析:
问题抽象:有向图的拓扑排序问题
具体来说:
-
将每门课程看作图中的一个节点。
-
如果课程
a依赖于课程b(即[a, b]),则在图中添加一条从b指向a的有向边。
这样,问题就转化为:判断这个有向图是否存在拓扑排序,即图中是否存在环。如果图中存在环,则无法完成所有课程(因为存在循环依赖);否则可以完成。
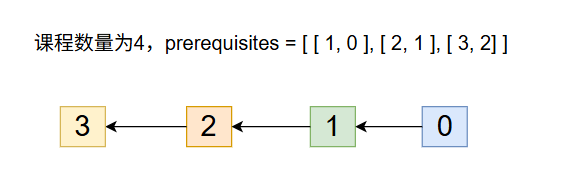
举两个例子:
无环:
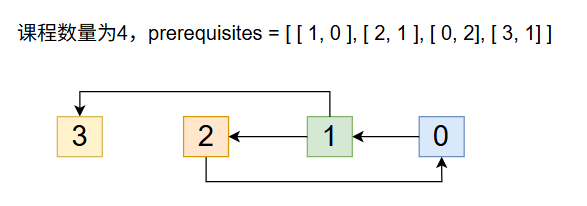
有环:
代码的实现思路:(基于入度)
-
统计入度:对于每个课程,统计它的入度(即有多少课程依赖于它)。这里
rdegree数组记录的是每个课程的入度(即依赖的课程数量),使用一个map记录课程的依赖关系。 -
初始化队列:将所有入度为 0 的节点加入队列。这些课程没有先修课程,可以直接学习。
-
拓扑排序过程:
-
从队列中取出一个课程,将其“完成”(
count++)。 -
遍历该节点依赖于它的课程,将它们的入度减 1(表示依赖关系被满足)。
-
如果某个课程的入度减为 0,则将其加入队列(表示可以开始学习)。
-
-
判断结果:如果最终完成的课程数量等于总课程数量(
count == numCourses),则说明可以完成所有课程(图中无环);否则不能完成(图中有环)。
具体代码实现:
bool canFinish(int numCourses, vector<vector>& prerequisites) { vector rdegree(numCourses); //用于记录节点入度的信息 unordered_map<int, vector> mp; //记录一门的课程的前驱课程有哪些 // 构建入度数组和邻接表 for(int i = 0; i < prerequisites.size(); i++){ rdegree[prerequisites[i][0]]++; mp[prerequisites[i][1]].push_back(prerequisites[i][0]); } queue que; int count = 0; //将所有入度为0的课程加入队列中 for(int i = 0; i 0){ rdegree[it] --; //如果入度为0就要加入队列 if(rdegree[it] == 0){ que.push(it); } } } } //判断一下被处理的节点数和总结点数是否相同 if(count == numCourses){ return true; } return false; }复杂度分析:
-
时间复杂度:O(N + E),其中 N 是课程数量,E 是先修关系的数量(即边的数量)。需要遍历所有节点和边。
-
空间复杂度:O(N + E),用于存储邻接表和入度数组。