网站导航
> 技术文档 > 广义优势估计的推导

广义优势估计的推导

网友: 技术文档 2025-07-26 20:00:41

总结

       广义优势估计是对多步时序差分误差的指数加权平均.

指数加权平均

      对于一组数字x_n, x_{n-1}, x_{n-2}, ..., x_1 计算指数加权平均Y_i = \\lambda Y_{i-1} + (1-\\lambda)x_i, 其中i是下标. 那么有

 Y_1 = (1-\\lambda)x_1 \\\\ Y_2 = \\lambda Y_1 + (1- \\lambda) x_2 = \\lambda (1-\\lambda)x_1 + (1- \\lambda) x_2\\\\ Y_3 = \\lambda Y_2 + (1- \\lambda) x_3 = \\lambda^2 (1-\\lambda)x_1 + \\lambda(1-\\lambda) x_2 + (1- \\lambda) x_3\\\\ Y_{n-1} = \\lambda Y_{n-2} + (1- \\lambda) x_{n-1} = (1-\\lambda) (\\lambda^{n-2}x_1 + \\lambda^{n-3}x_2 + ... + \\lambda^0 x_{n-1}) \\\\ Y_{n-0} = \\lambda Y_{n-1} + (1- \\lambda) x_{n} = (1-\\lambda) (\\lambda^{n-1}x_1 + \\lambda^{n-2}x_2 + ... + \\lambda^0 x_{n}) \\\\

        把x_n, x_{n-1}, x_{n-2}, ..., x_1按照下标顺序代入, 

Y_1 = (1-\\lambda)x_n \\\\ Y_2 = \\lambda Y_1 + (1- \\lambda) x_{n-1} = \\lambda (1-\\lambda)x_n + (1- \\lambda) x_{n-1}\\\\ Y_3 = \\lambda Y_2 + (1- \\lambda) x_{n-2} = \\lambda^2 (1-\\lambda)x_n + \\lambda(1-\\lambda) x_{n-1} + (1- \\lambda) x_{n-2}\\\\ Y_{n-1} = \\lambda Y_{n-2} + (1- \\lambda) x_{2} = (1-\\lambda) (\\lambda^{n-2}x_n + \\lambda^{n-3}x_{n-1} + ... + \\lambda^0 x_{2}) \\\\ Y_{n-0} = \\lambda Y_{n-1} + (1- \\lambda) x_{1} = (1-\\lambda) (\\lambda^{n-1}x_n + \\lambda^{n-2}x_{n-1} + ... + \\lambda^0 x_{1}) \\\\ 

多步时序差分误差 

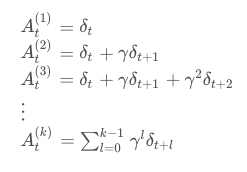
    分别是t时刻的 一步误差, 两步误差, 三步误差, ... k步误差. 把这些步的误差倒过来代入指数加权公式,就得到了该时刻的GAE. 

GAE的计算

    考虑t时刻的无穷步误差的指数加权, 有

   

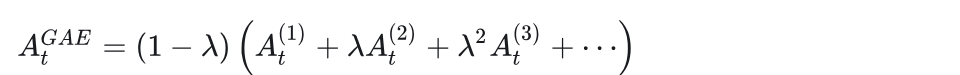
把A_t^{()}代入,然后重新拆分得到

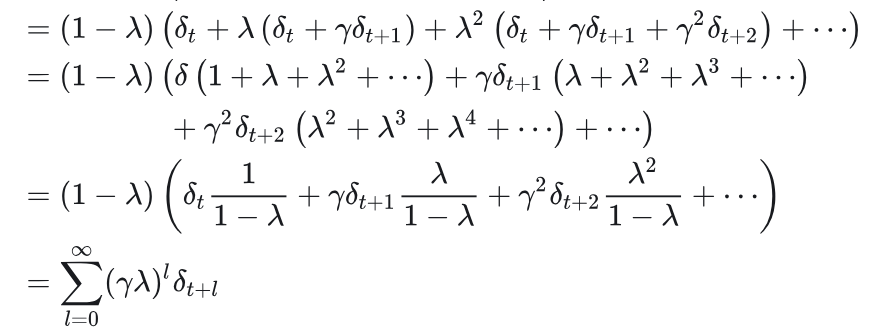
 =\\delta_t + \\gamma \\lambda \\sum_{l=0}^{\\infty }( \\gamma \\lambda)^l \\delta_{t+1+l} \\\\ = \\delta_t + \\gamma \\lambda A_{t+1}^{GAE}

可见GAE的递推公式, 可以利用该公式, 从后往前一次性算出所有时刻的GAE.

 def compute_gae_and_returns( rewards: torch.Tensor, values: torch.Tensor, next_values: torch.Tensor, dones: torch.Tensor, discount_rate: float, lambda_gae: float, ) -> Tuple[torch.Tensor, torch.Tensor]: advantages = torch.zeros_like(rewards) last_advantage = 0.0 n_steps = len(rewards) # 计算GAE for t in reversed(range(n_steps)): mask = 1.0 - dones[t] delta = rewards[t] + discount_rate * next_values[t] * mask - values[t] advantages[t] = delta + discount_rate * lambda_gae * last_advantage * mask last_advantage = advantages[t] # 返回给critic作为TD目标 returns_to_go = advantages + values return advantages, returns_to_go
网络标签：

相关问题