【AI中数学-概率论】拉普拉斯分布:尖峰与重尾的叙事_重尾分布图像
第20节 拉普拉斯分布:尖峰与重尾的叙事
拉普拉斯分布(Laplace Distribution)是一种对称的概率分布,具有尖峰状的概率密度函数和相对较厚的尾部。它在许多实际应用中扮演着重要的角色,尤其在涉及稀有事件或较大波动的情况时。由于其尾部的厚重特性,拉普拉斯分布能够有效地描述那些波动较大或极端事件出现频率较高的现象。本文将通过AI应用中的金融市场风险建模、图像噪声建模和自然语言错误检测进行详细说明。
拉普拉斯分布的概率密度函数(PDF)可以表示为:
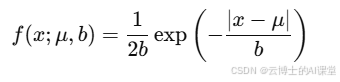
其中,μ 是位置参数(即分布的中心),b 是尺度参数,决定了分布的“宽度”或波动范围。与正态分布相比,拉普拉斯分布的尾部更重,即在远离均值的地方,数据的概率密度依然较大。
20.1 拉普拉斯分布的性质与特点
- 对称性:拉普拉斯分布是对称的,其均值 μ 是分布的中心。
- 尖峰特性:由于拉普拉斯分布的概率密度函数在均值附近迅速下降,它有一个尖锐的峰值,表示在均值附近发生事件的概率较高。
- 重尾特性:拉普拉斯分布的尾部相对于正态分布来说较重,这使得其能够更好地描述极端值或稀有事件的出现。
- 均值与方差:
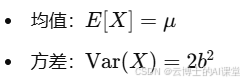
20.2 拉普拉斯分布的应用场景
由于其特有的尖峰与重尾特性,拉普拉斯分布在多个领域有广泛应用,包括但不限于:
- 金融领域:拉普拉斯分布可以用来建模金融市场的价格波动,尤其是股票和资产的极端波动。
- 信号处理:拉普拉斯分布可以用于建模噪声,特别是在数据中存在较大波动或偶发事件时。
- 图像处理与压缩:在图像处理中,拉普拉斯分布常常用来描述图像中像素值的差异,尤其在压缩算法中得到广泛应用。
20.3 AI应用中的拉普拉斯分布案例
1. 金融市场中的风险建模
在金融市场中,拉普拉斯分布常常用来建模股票价格的波动性。与正态分布相比,拉普拉斯分布的尾部较厚,能够更好地捕捉到市场中出现的极端波动,如股市崩盘或暴涨。
假设问题:某股票的日收益率 rr 服从拉普拉斯分布,均值 μ=0,尺度参数 b=0.02。我们希望计算该股票在一天内的收益率超过 0.05 的概率。
计算过程:

应用场景总结: 在金融市场的风险管理中,使用拉普拉斯分布可以帮助捕捉到那些不常发生但影响巨大的极端波动,提供更为精确的风险评估。
2. 图像处理中的噪声建模
在图像处理中,尤其是在图像压缩或去噪过程中,拉普拉斯分布常常被用来建模图像像素值的差异。图像中许多自然的噪声现象,如椒盐噪声,常常呈现出重尾分布,适合使用拉普拉斯分布来建模。
假设问题:某图像的像素值差异(两个相邻像素的灰度差)服从拉普拉斯分布,均值为 0,尺度参数 b=5。我们希望计算两个相邻像素的灰度差大于 10 的概率。
计算过程:

应用场景总结: 在图像去噪和压缩的过程中,拉普拉斯分布提供了一种高效的方式来建模图像像素的差异,能够帮助我们有效处理图像中的噪声,改善图像质量。
3. 自然语言处理中的错误检测
在自然语言处理(NLP)任务中,尤其是在自动拼写检查或文本错误检测中,拉普拉斯分布可以用来建模词语之间的差异或错误的出现概率。例如,在自动拼写纠错中,单词的错误通常可以视为遵循拉普拉斯分布的随机过程,错误的频率随着单词的频繁程度而减小。
假设问题:某自然语言处理中,某个常见单词的拼写错误发生间隔服从拉普拉斯分布,均值为 0,尺度参数 b=0.1。我们希望计算该单词拼写错误发生间隔大于 0.3 的概率。
计算过程:

应用场景总结: 在拼写错误的检测和纠正中,拉普拉斯分布的应用帮助我们合理预测错误出现的间隔,进而优化拼写纠错模型。例如,如果错误频繁发生,模型可能会通过这种概率分布及时发现并纠正错误,从而提高文本的准确性和可读性。
20.4 拉普拉斯分布的总结与展望
拉普拉斯分布作为一种具有尖峰和重尾特性的概率分布,能够有效地捕捉到那些偶发且极端的事件。其在金融风险建模、图像处理、自然语言处理等地方的应用,展示了它在解决实际问题中的强大能力。在这些领域,拉普拉斯分布能够提供更好的描述那些不常发生但又有重要影响的极端波动或变化。
随着机器学习和人工智能的进一步发展,拉普拉斯分布的应用潜力将进一步得到发掘。例如,在大规模数据处理中,拉普拉斯分布可能会成为处理噪声、异常值和突发事件的重要工具,特别是在那些要求对稀有事件做出快速响应的任务中。此外,结合深度学习中的生成模型(如变分自编码器),拉普拉斯分布能够为图像生成、自然语言生成等任务提供更加精准的建模能力。
总之,拉普拉斯分布不仅是一种强有力的数学工具,它也将成为未来多种AI应用中不可或缺的组成部分。理解和掌握拉普拉斯分布的理论与应用,能够帮助我们更好地处理和理解各种数据中的极端情况,提升AI系统的性能和可靠性。
通过这一节的学习,我们深入了解了拉普拉斯分布的定义、性质、应用领域,并通过具体的计算例子展示了它在金融、图像处理和自然语言处理中的实际应用。拉普拉斯分布的尖峰和重尾特性使其在很多实际问题中具有不可替代的作用,特别是在那些关注极端事件或异常波动的场景中,拉普拉斯分布为我们提供了一个有效的建模工具。


