手写A2C(FrozenLake环境)

成功截图

算法组件

包含: 包含经验池, actor_model, critic_model三个部分

• actor输出每一个state对应所有action的概率 --- 概率分布
• critic估计每一个状态的状态值 --- 标量

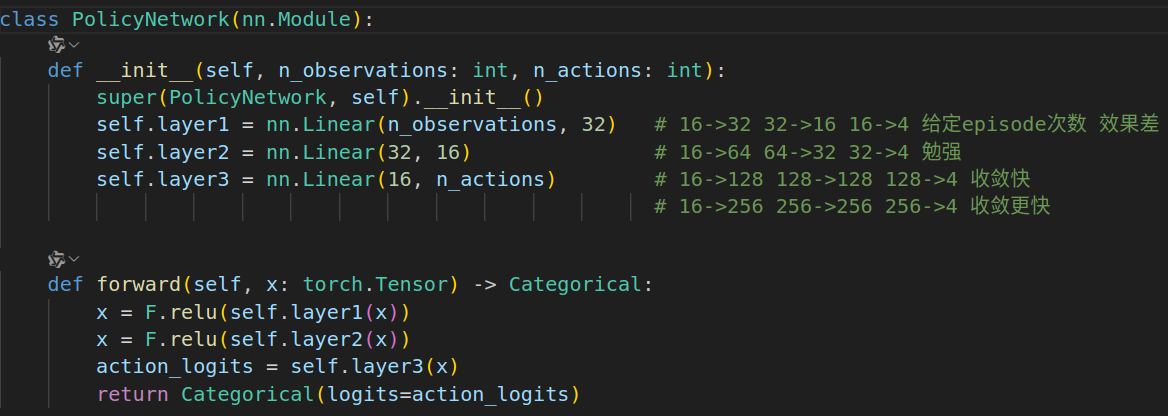
actor和critic都用mlp, 经过试验发现actor的网络复杂一点效果好一些.

actor最后输出的torch.distributions.Categorical类是一个概率分布类, 用于处理类别分布(离散分布), 有如下的作用:

• 自动应用softmax函数, 将输入logits转为归一化的概率分布
• 方便从该分布中采样: sample()方法
• 方便计算给定样本的概率 对数概率 熵: probs() log_prob() entropy() 方法

训练框架

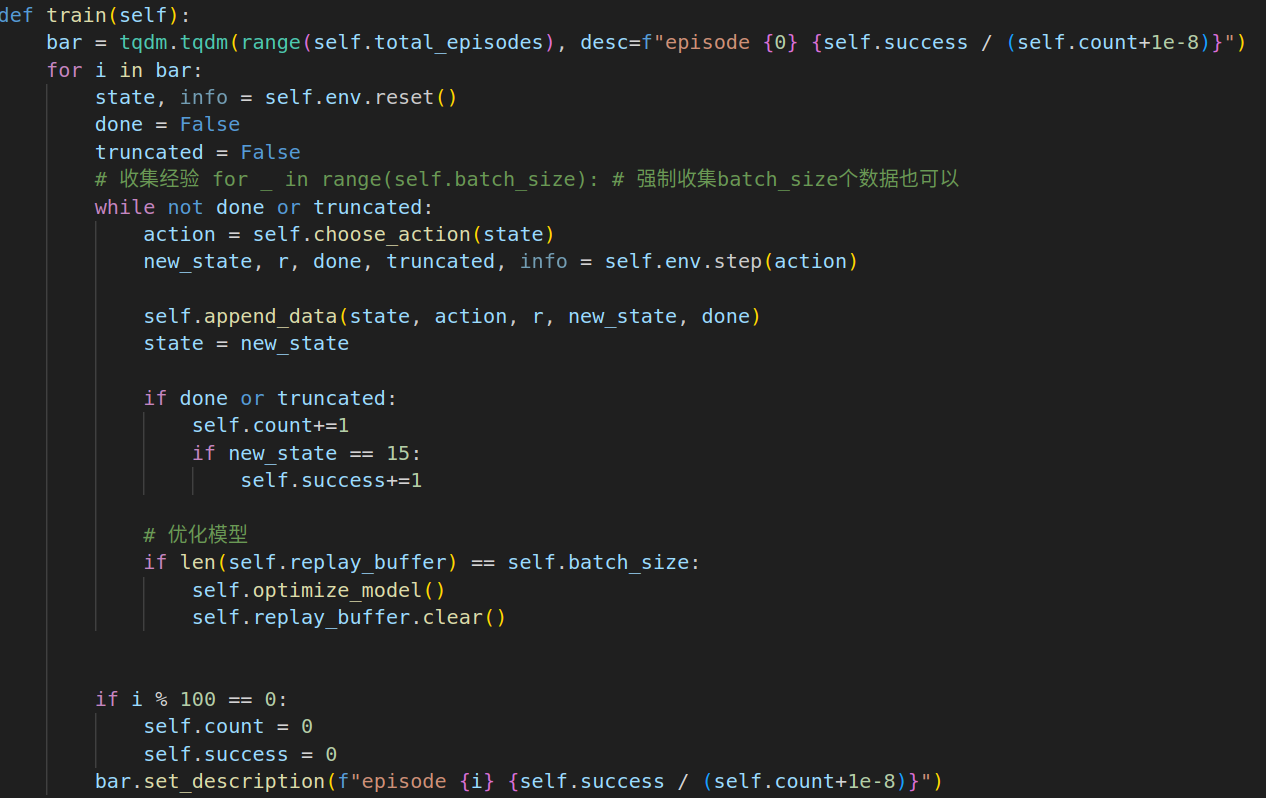
• 先收集经验,然后优化模型, 这里当收集够一个批次后就优化模型
• 由于a2c是on-policy算法, replay buffer 收集后使用就不用了, 所以优化模型后就清空

目标函数

1. actor用策略梯度定理

其中A采用广义优势估计, 效果要好一些

2. critic用目标值和当前值的MSE

目标值 = 当前值+广义优势估计

3. 广义优势估计计算

完整代码

import torchimport torch.nn as nnfrom torch.nn import functional as Fimport gymnasium as gymimport tqdmfrom torch.distributions import Categoricalfrom typing import Tupleclass PolicyNetwork(nn.Module): def __init__(self, n_observations: int, n_actions: int): super(PolicyNetwork, self).__init__() self.layer1 = nn.Linear(n_observations, 32) # 16->32 32->16 16->4 给定episode次数 效果差 (在self.lr = 0.0001下,但是在self.lr = 0.01 照样能收敛 ) self.layer2 = nn.Linear(32, 16)  # 16->64 64->32 32->4 勉强 self.layer3 = nn.Linear(16, n_actions) # 16->128 128->128 128->4 收敛快 # 16->256 256->256 256->4 收敛更快 def forward(self, x: torch.Tensor) -> Categorical: x = F.relu(self.layer1(x)) x = F.relu(self.layer2(x)) action_logits = self.layer3(x) return Categorical(logits=action_logits) class A2C: def __init__(self, env, total_episodes): #############超参数############# self.actor_lr = 0.01 self.critic_lr = 0.01 self.batch_size = 256 self.entropy_coeff = 0.01 self.value_loss_coeff = 0.5 self.gae_lambda = 0.95 self.discount_rate = 0.99 self.total_episodes = total_episodes #############A2C的核心要件############# self.replay_buffer = [] self.actor_model = PolicyNetwork(16, 4) self.critic_model = nn.Sequential( # 不需要像 actor model那么复杂 nn.Linear(16, 16), nn.ReLU(), nn.Linear(16, 1) ) ############优化组件############# self.actor_optimizer = torch.optim.Adam(self.actor_model.parameters(), lr=self.actor_lr) self.critic_optimizer = torch.optim.Adam(self.critic_model.parameters(), lr=self.critic_lr) self.env = env self.count = 0 self.success = 0 def train(self): bar = tqdm.tqdm(range(self.total_episodes), desc=f\"episode {0} {self.success / (self.count+1e-8)}\") for i in bar: state, info = self.env.reset() done = False truncated = False # 收集经验 for _ in range(self.batch_size): # 强制收集batch_size个数据也可以 while not done or truncated: action = self.choose_action(state) new_state, r, done, truncated, info = self.env.step(action)  self.append_data(state, action, r, new_state, done) state = new_state if done or truncated:  self.count+=1  if new_state == 15: self.success+=1 # 优化模型 if len(self.replay_buffer) == self.batch_size:  self.optimize_model()  self.replay_buffer.clear()  if i % 100 == 0: self.count = 0 self.success = 0 bar.set_description(f\"episode {i} {self.success / (self.count+1e-8)}\") def choose_action(self, state): with torch.no_grad(): policy_dist = self.actor_model(self.state_to_input(state)) action_tensor = policy_dist.sample() action = action_tensor.item() return action def optimize_model(self): state = torch.stack([self.state_to_input(tup[0]) for tup in self.replay_buffer[-self.batch_size:]]) action = torch.IntTensor([tup[1] for tup in self.replay_buffer[-self.batch_size:]]) reward = torch.FloatTensor([tup[2] for tup in self.replay_buffer[-self.batch_size:]]) new_state = torch.stack([self.state_to_input(tup[3]) for tup in self.replay_buffer[-self.batch_size:]]) done = torch.FloatTensor([tup[4] for tup in self.replay_buffer[-self.batch_size:]]) # 以上state和new_state是二维的, 其他是一维的,即batch维 with torch.no_grad(): value = self.critic_model(state).squeeze() last_value = self.critic_model(new_state[:-1]).squeeze() next_value = torch.cat((value[1:], last_value)) # 相比一次TD误差, GAE效果显著之好 advantages, returns_to_go = self.compute_gae_and_returns( reward, value, next_value, done,  self.discount_rate, self.gae_lambda ) # 更新actor 根据策略梯度定理 policy_dist = self.actor_model(state) logpi = policy_dist.log_prob(action)  actor_fn = -(logpi * advantages + self.entropy_coeff * policy_dist.entropy()) # 熵的效果不大 self.actor_optimizer.zero_grad() actor_fn.mean().backward(retain_graph=True) # .mean() torch要求梯度得标量函数 self.actor_optimizer.step() # 更新critic v = self.critic_model(state).squeeze() critic_fn = F.mse_loss(v, returns_to_go) self.critic_optimizer.zero_grad() (self.value_loss_coeff * critic_fn).backward() self.critic_optimizer.step() def compute_gae_and_returns(self, rewards: torch.Tensor, values: torch.Tensor, next_values: torch.Tensor, dones: torch.Tensor, discount_rate: float, lambda_gae: float, ) -> Tuple[torch.Tensor, torch.Tensor]: advantages = torch.zeros_like(rewards) last_advantage = 0.0 n_steps = len(rewards) # 计算GAE for t in reversed(range(n_steps)): mask = 1.0 - dones[t] delta = rewards[t] + discount_rate * next_values[t] * mask - values[t] advantages[t] = delta + discount_rate * lambda_gae * last_advantage * mask last_advantage = advantages[t] # 返回给critic作为TD目标 returns_to_go = advantages + values return advantages, returns_to_go def append_data(self, state, action, r, new_state, done): self.replay_buffer.append((state, action, r, new_state, done)) def state_to_input(self, state): input_dim = 16 input = torch.zeros(input_dim, dtype=torch.float) input[int(state)] = 1 return input env = gym.make(\"FrozenLake-v1\", is_slippery=False)policy = A2C(env, 3000)policy.train()env = gym.make(\"FrozenLake-v1\", is_slippery=False, render_mode=\"human\")state, info = env.reset()done = Falsetruncated = Falsewhile True: with torch.no_grad(): action=policy.choose_action(state) new_state, reward, done, truncated, info = env.step(action) state=new_state if done or truncated: state, info = env.reset()

调参体会

• lr还是很有影响
• actor的模型复杂度影响也有影响,体会到了复杂mlp比简单的mlp效果要好
• 最有效果的是GAE替代了一次TD误差