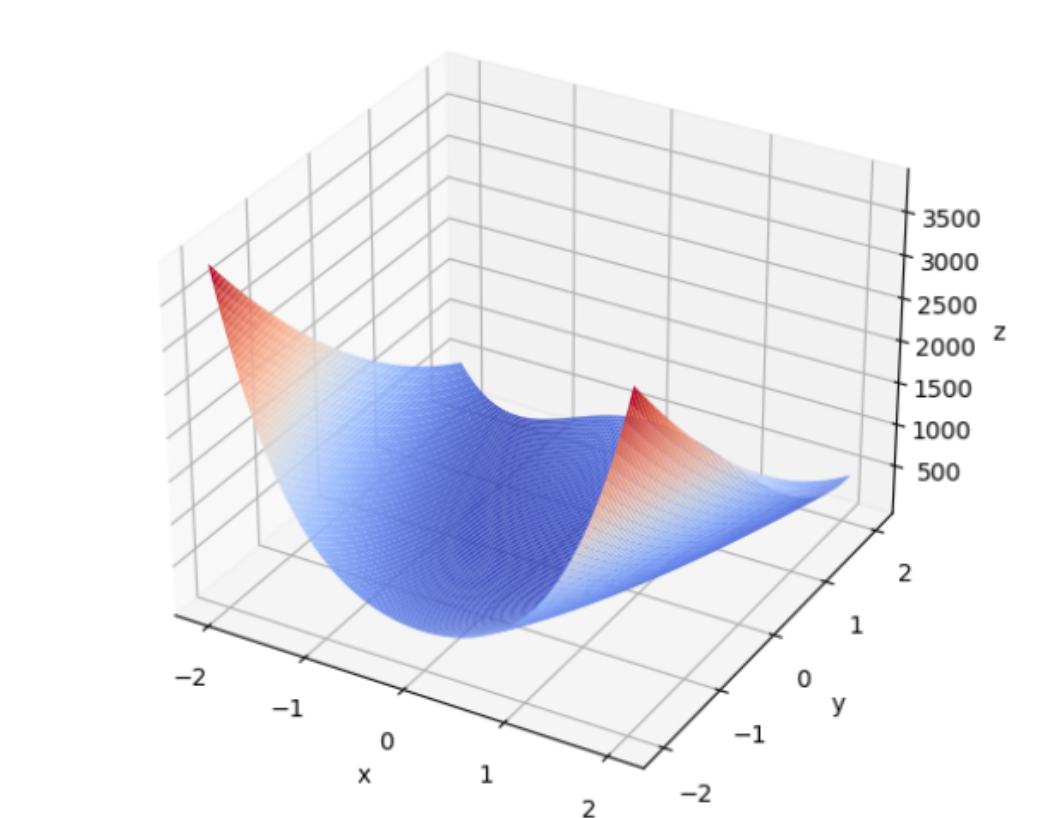
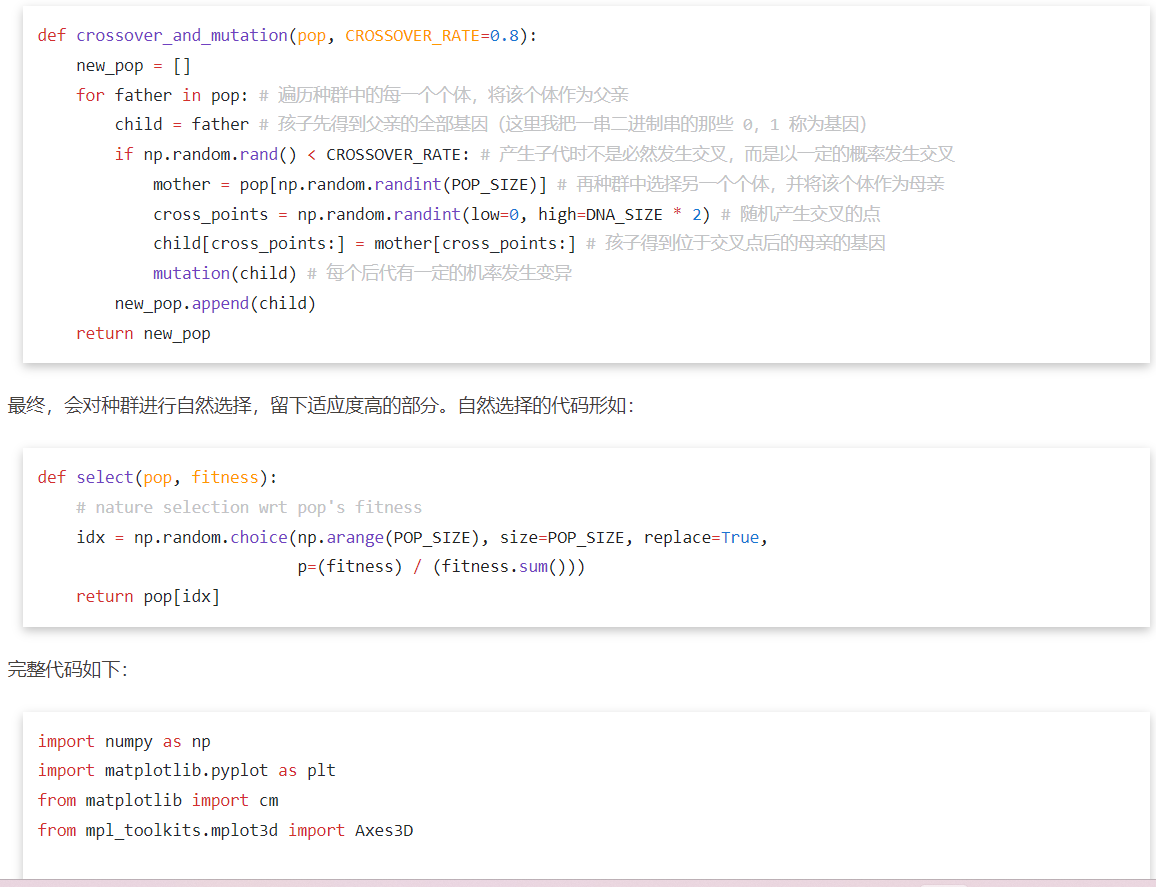
进化计算与群体智能（数学建模理论与python）_群智能算法 进化计算

第5章 进化计算与群体智能
 
一、引言
 
（一）核心概念引入
 
进化计算与群体智能是人工智能领域模仿自然生物机制求解复杂问题的方法集合。受生物进化（如遗传变异）、群体协作（如蚁群觅食）启发，为优化计算、智能决策等提供新思路，弥补传统算法在复杂空间寻优的不足 。
 
（二）应用场景概览
 
广泛用于工程优化（如电路设计、机械结构优化 ）、路径规划（物流配送、机器人运动 ）、机器学习（超参数优化、特征选择 ）等地方，解决传统方法难以高效处理的多约束、多目标复杂问题。
 
二、5.1 遗传算法理论与实现
 
（一）理论基础——模拟生物进化
 
核心机制
 
- 遗传操作：模拟生物遗传，包含选择（依据适应度选优秀个体，如轮盘赌选择，按适应度概率选父代 ）、交叉（类似基因重组，如单点交叉，交换染色体片段产生新个体 ）、变异（随机改变基因位，保持种群多样性，避免早熟收敛 ）。
 
- 种群与适应度：种群是个体集合，个体以染色体编码（如二进制、实数编码 ），适应度函数评估个体对环境“适配性”，指导进化方向。
 
数学模型简化理解：把优化问题解编码为“染色体”，通过迭代的遗传操作，在解空间搜索，使种群适应度逐步提升，逼近最优解，类似生物“适者生存”筛选优质解。
 
（二）实现步骤与要点
 
流程框架：初始化种群（随机生成一定数量编码个体 ）→计算适应度→遗传操作（选择、交叉、变异 ）→迭代更新种群，直到满足停止条件（如迭代次数、适应度阈值 ）。
 
关键细节
 
- 编码方式选择：二进制编码适合离散问题，实数编码适配连续优化，需依问题特性选，影响算法效率与精度。
 
- 参数调优：种群规模（过小易早熟，过大计算量大 ）、交叉率（过高破坏优质基因，过低进化慢 ）、变异率（过低难创新，过高成随机搜索 ），需实验调试平衡。
 
（三）典型应用示例
 
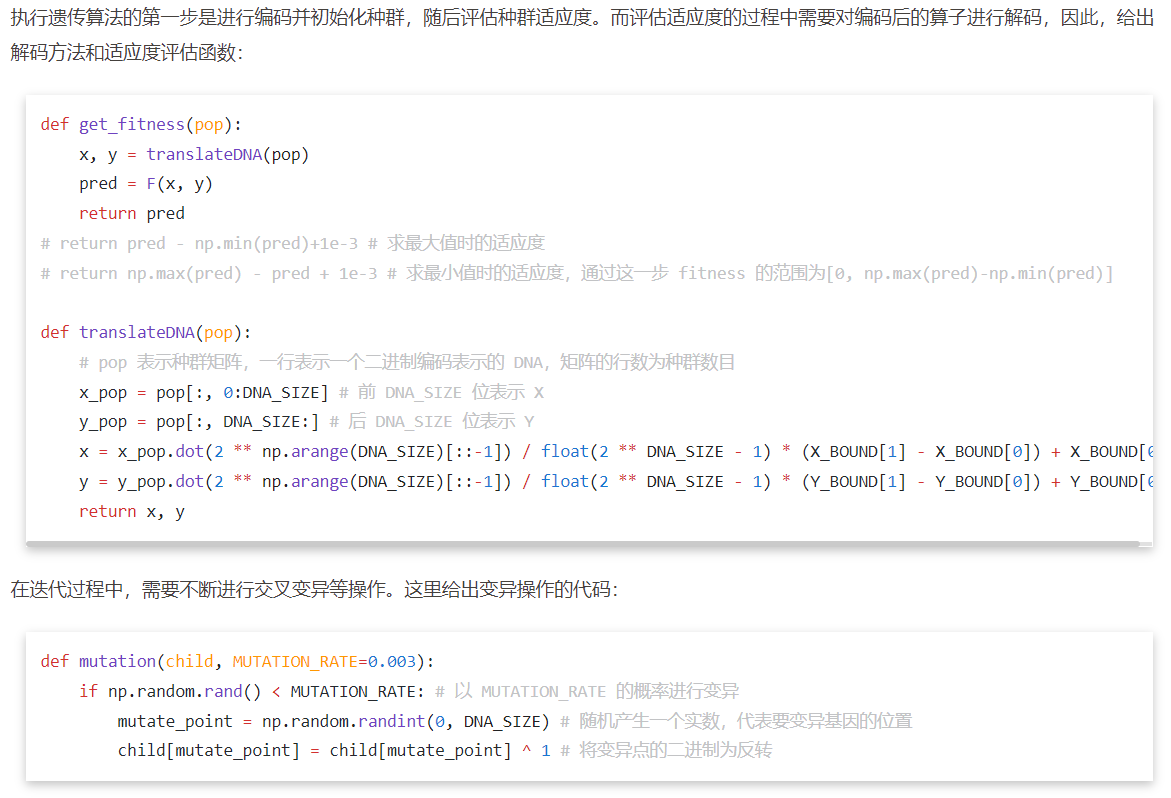
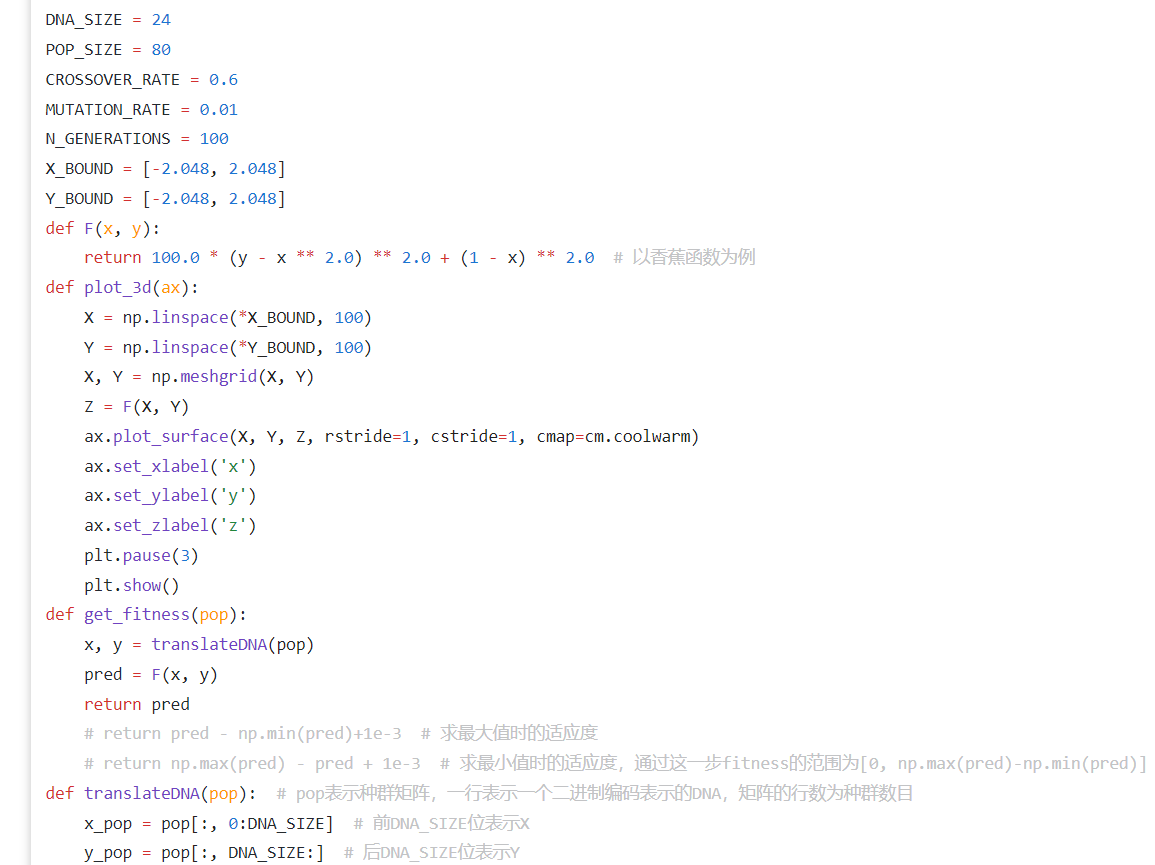
在函数优化中，如求复杂多峰函数最优值，遗传算法通过种群进化跳出局部最优；在旅行商问题（TSP）里，编码城市序列为染色体，交叉变异探索更短路径，是解决组合优化经典案例 。
 
三、5.2 粒子群算法理论与实现
 
（一）理论基础——模拟群体协作
 
核心机制：模拟鸟群、鱼群等群体行为，粒子在解空间飞行，通过个体历史最优（pbest）和群体历史最优（gbest）调整速度与位置。速度更新公式含自身认知项（跟踪个体最优 ）、社会协作项（学习群体最优 ），位置依速度迭代更新，实现寻优。
 
数学表达简化：速度公式  v_{id} = \\omega v_{id} + c_1 r_1 (p_{id} - x_{id}) + c_2 r_2 (g_{d} - x_{id})  ，位置公式  x_{id} = x_{id} + v_{id}  。其中\\omega是惯性权重（平衡全局与局部搜索 ），c_1,c_2是学习因子（控制个体与群体学习强度 ），r_1,r_2是随机数增加随机性。
 
（二）实现流程与特点
 
执行步骤：初始化粒子群（随机位置、速度 ）→计算粒子适应度→更新个体与群体最优→迭代调整速度位置，直至收敛。
 
算法优势与局限
 
- 优势：实现简单，收敛快，适合连续空间优化；群体协作能快速探索解空间，在多峰函数、动态优化中表现好。
 
- 局限：易陷入局部最优（后期粒子趋同 ）；参数敏感（惯性权重、学习因子需精细调 ），对离散问题适配性弱（需改进编码 ）。
 
（三）实际应用场景
 
在电力系统优化（如机组组合、无功优化 ）中，粒子群算法快速寻优降低能耗；无人机编队控制里，优化飞行路径与队形，通过群体协作适应动态环境，是群体智能在工程实践的典型应用 。
 
三、5.3 蚁群算法理论与实现
 
（一）理论灵感——蚁群觅食行为
 
核心机制：模拟蚂蚁分泌信息素、跟随信息素路径觅食的行为。蚂蚁在路径上释放信息素，信息素浓度引导路径选择，同时信息素会挥发。路径越短，蚂蚁往返越快，信息素积累越多，形成正反馈，逐步找到最优路径（如蚁群找最短觅食路径 ）。
 
数学模型关键
 
- 信息素更新：包含局部更新（蚂蚁移动时少量挥发，保持探索性 ）与全局更新（最优路径蚂蚁强化信息素，突出优质解 ）。
 
- 转移概率：蚂蚁依据路径信息素浓度、启发式信息（如距离倒数，引导向近邻节点 ）选择下一个节点，公式平衡信息素与启发式引导，控制搜索方向。
 
（二）实现逻辑与优化点
 
基本流程：初始化蚁群与信息素矩阵→蚂蚁遍历节点（按转移概率选路径 ）→完成路径后更新信息素→迭代直至路径稳定。
 
优化挑战与应对
 
- 早熟收敛：信息素集中导致搜索停滞，可通过限制信息素范围、引入随机因子扰动路径选择解决。
 
- 计算效率：蚁群规模大时计算量大，可优化信息素更新策略（如仅更新关键路径 ）、并行计算加速遍历过程。
 
（三）经典应用领域
 
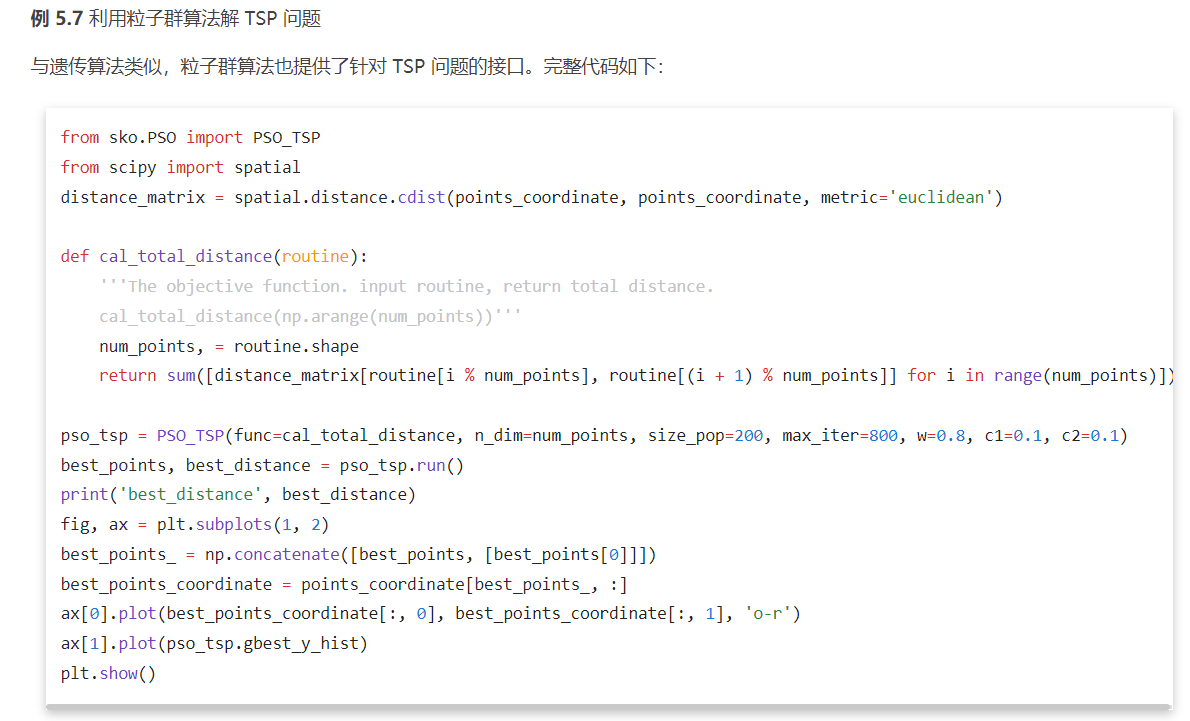
在旅行商问题（TSP）及扩展（多旅行商、带时间窗 ）中，蚁群算法通过信息素协作高效寻优；物流配送路径规划、电网路由优化等场景，利用其群体协作、动态适应能力，解决复杂网络路径选择问题 。
 
四、5.4 模拟退火算法理论与实现
 
（一）理论溯源——模拟物理退火
 
核心机制：模仿金属退火“加热 - 缓慢冷却”过程，以概率接受劣解。在解空间随机搜索，当温度高时，大概率接受劣解（探索新区域 ）；温度降低，接受劣解概率减小（收敛到优质解 ）。通过控制温度衰减（如指数降温 ），平衡探索与利用，避免陷入局部最优。
 
数学表达核心
 
- Metropolis准则：若新解f(new)优于当前解f(current)，直接接受；若更差，以概率 P = e^{-\\frac{f(new) - f(current)}{T}}  接受，T是当前温度，温度决定接受劣解可能性。
 
（二）实现关键与策略
 
流程架构：初始化解与温度→随机扰动生成新解→用Metropolis准则判断是否接受→降温→迭代至温度足够低。
 
参数与策略优化
 
- 温度调度：初始温度要足够高（保证探索广度 ），降温速率需合理（如线性、几何降温 ），过慢计算耗时，过快易早熟。
 
- 解的扰动：依问题选扰动方式（如函数优化中随机增减变量值 ），既要改变解状态，又需控制变化幅度，维持搜索有效性。
 
（三）应用场景与优势
 
在工程优化（如集成电路布局、神经网络权值优化 ）中，处理多局部最优问题，模拟退火通过概率接受劣解跳出陷阱；在组合优化（如车间调度 ）里，应对解空间复杂、传统方法难寻优场景，利用其单个体搜索、无需群体协作的灵活性，适配小规模、高精度优化需求 。
 
五、5.5 使用scikit - opt实现（以补充完整场景为例，假设是用工具实现上述算法 ）
 
（一）工具适配逻辑
 
scikit - opt是Python优化算法工具库，封装遗传算法、粒子群算法等实现。其优势是简化算法编码，通过统一接口调用，内置参数默认配置，降低开发门槛。支持自定义适应度函数、编码方式，适配不同问题场景。
 
（二）典型实现步骤（以遗传算法为例 ）
 
环境准备：安装scikit - opt库（如 pip install scikit - opt  ），导入相关模块（如 from sko.GA import GA  ）。
 
问题定义：编写适应度函数（如优化函数 f(x) = x^2 ，返回值评估解优劣 ），确定变量范围（如 x \\in [-10,10]  ）。
 
算法调用：初始化GA对象（设置种群规模、迭代次数、变量维度等参数 ），调用 run() 方法执行，获取最优解与最优适应度，如 best_x, best_y = ga.run()  ，便捷实现算法应用。
 
（三）工具价值与拓展
 
scikit - opt让算法实现“低代码化”，适合快速验证算法逻辑、搭建原型系统。同时支持与其他库（如NumPy做数值计算、Matplotlib可视化迭代过程 ）结合，拓展分析维度。在教学演示、小规模项目开发中，能高效落地进化计算与群体智能算法，降低技术应用门槛 。