Unity基础学习（九）基本组件Transform_unity transform

目录

引言：Transform是什么？有哪些重要内容，为什么说它很重要？

前置知识：Unity中的三维向量Vector2/3类，这里只介绍Vector3，2和3是类似的，只是名字不一样

 常用静态属性（预定义值）

一、位置和位移

1、世界坐标系位置（World Space）：对象相对于 场景原点（0,0,0） 的绝对坐标。

2、自身坐标系位置：对象相对于 父对象原点 的坐标（若无父对象，等同于世界坐标）。

图片示例：

（1）父对象自己的世界坐标位置

（2）子对象面板为0时的Position位置：

​编辑 （3）相对于父对象偏移后的位置：

（4）实际的世界坐标位置：（17,5,5）= （12,0,0）+（5,5,5）

3、一些注意点

（1）不可单独修改坐标分量

（2）对象的朝向属性

（3）父子层级的影响

4、位移

方式一：手动计算并修改Position

方式二：使用Transform.Translate方法

参数组合效果

二、角度和旋转

图示：

（1）我们创建三个用于演示不同角度变化的平面，其中不同的颜色代表等会改变那个方向上的角度

（2） 首先我们改变沿x轴方向的角度，可以看出实际上就是将于X轴不相关的另外两个轴组成的平面发生了旋转，围绕着X轴转。

（3）旋转另外两个轴的角度，黑色的是不作任何处理

相关参数和使用方法：    

1. 世界坐标系与本地坐标系角度

       2. 旋转的两种实现方式：这里和位置是及其类似的，所以不再解释原理，直接上方法！不过值得注意的是，我们在这里不会选择自己手动实现通过改变面板上数值的方式旋转，而是通过API

1. 自转：Rotate 方法

方式一：指定旋转向量

方式二：指定轴和角度

2. 绕点旋转：RotateAround 方法

三、缩放和看向

缩放：

看向：顾名思义就是看向一个地方，一般是看向一个点。或者一个对象，这个很简单。有一个API提供给我们使用。

四、父子关系

        父子关系基础操作

1. 获取与设置父对象

2. 解除父子关系

        子对象操作

1. 获取子对象

2. 子对象顺序管理

Unity父子关系操作汇总表

父子关系基础操作

子对象操作

五、坐标转换

世界坐标转本地坐标

1. ​点的转换：InverseTransformPoint

2. ​方向的转换：InverseTransformDirection​

3. ​向量的转换：InverseTransformVector

本地坐标转世界坐标

1. ​点的转换：TransformPoint​

2. ​方向的转换：TransformDirection​

3. ​向量的转换：TransformVector​

六、总结

位置（Position）

位移（Movement）

角度与旋转（Rotation）

缩放（Scale）

父子关系（Parenting）

坐标转换（Space Conversion）

---

引言：Transform是什么？有哪些重要内容，为什么说它很重要？

        Transform是Unity中每个GameObject（游戏对象）的必备组件，用于定义对象在3D/2D空间中的位置（Position）、旋转（Rotation）、缩放（Scale）以及层级关系。它是所有游戏对象的“空间身份证”，没有Transform的物体无法存在于场景中。

前置知识：Unity中的三维向量Vector2/3类，这里只介绍Vector3，2和3是类似的，只是名字不一样

        Vector3 是Unity中表示三维向量的结构体（struct），用于描述3D空间中的 位置（点） 或 方向（向量）。几乎所有与3D坐标相关的操作（如移动、旋转、距离计算）都依赖Vector3。

        基本使用方式：像下面这样 就是创建了一个三维向量，这个向量的方向是从原点指向这个点的或者就是指空间中这个点的位置。

Vector3 position = new Vector3(1.0f, 2.5f, -3.0f);

两种用途：
位置：表示空间中的一个点（如物体坐标）。
方向：表示一个有方向的向量（如移动方向、法线方向）。 

在这里我们只简单了解最基本的几个方向向量和基本运算，后面在系统学习。

 常用静态属性（预定义值）

Vector3.zero // (0, 0, 0) → 原点Vector3.one // (1, 1, 1) → 单位缩放Vector3.forward // (0, 0, 1) → Z轴正方向（物体前方）Vector3.back // (0, 0, -1)Vector3.up // (0, 1, 0) → Y轴正方向（物体上方）Vector3.down // (0, -1, 0)Vector3.right // (1, 0, 0) → X轴正方向（物体右侧）Vector3.left // (-1, 0, 0)

可结合图形理解： 

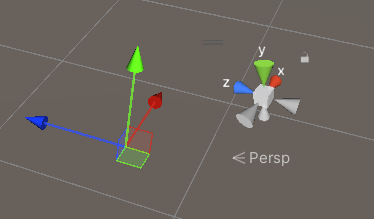
 基本运算 

// 向量加减Vector3 a = new Vector3(1, 2, 3);Vector3 b = new Vector3(4, 5, 6);Vector3 sum = a + b; // (5, 7, 9)Vector3 diff = a - b; // (-3, -3, -3)// 标量乘除Vector3 scaled = a * 2; // (2, 4, 6)Vector3 divided = a / 2; // (0.5, 1, 1.5)// 点积（Dot Product）→ 判断两向量夹角float dot = Vector3.Dot(a, b); // 叉积（Cross Product）→ 生成垂直于两向量的新向量Vector3 cross = Vector3.Cross(a, b); // 向量长度（模长）float magnitude = a.magnitude;// 单位化向量（方向不变，长度为1）Vector3 normalized = a.normalized;//计算两个点之间距离的方法Vector3.Distance(a, b);

一、位置和位移

这个Position是我们的主要研究对象

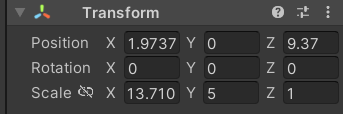
位置主要分为两块：

1、世界坐标系位置（World Space）：对象相对于 场景原点（0,0,0） 的绝对坐标。

Vector3 worldPos = transform.position;

设置方式：

transform.position = new Vector3(10, 0, 5); // 直接赋值

       注意事项：
若对象有父级且父级不在原点，position 与面板显示的 Local Position 不同。
修改 position 会直接改变对象的全局位置，无视父级影响。

2、自身坐标系位置：对象相对于 父对象原点 的坐标（若无父对象，等同于世界坐标）。

Vector3 localPos = transform.localPosition;

设置方式：

transform.localPosition = Vector3.up * 10; // 沿父对象Y轴移动

        与世界坐标的关系：
当父对象位于原点 且无旋转缩放 时，localPosition 与 position 相同。
若对象无父级，localPosition 直接等同于 position。

图片示例：

（1）父对象自己的世界坐标位置

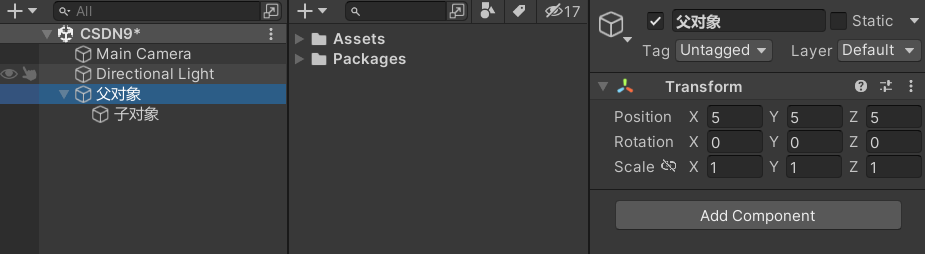
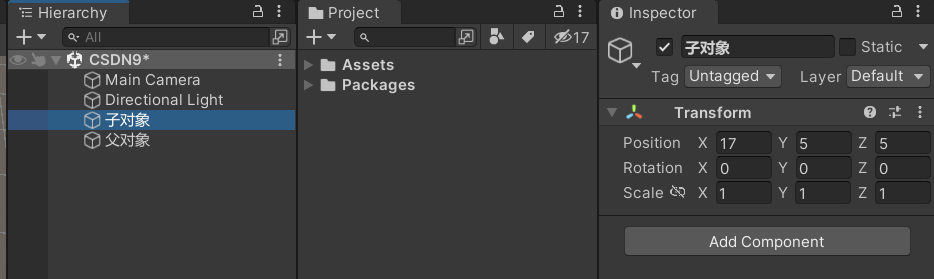
（2）子对象面板为0时的Position位置：

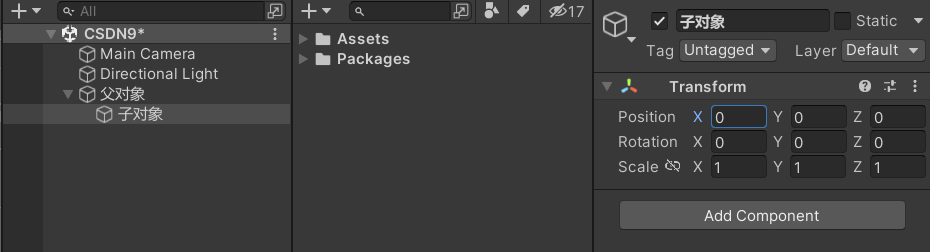 （3）相对于父对象偏移后的位置：

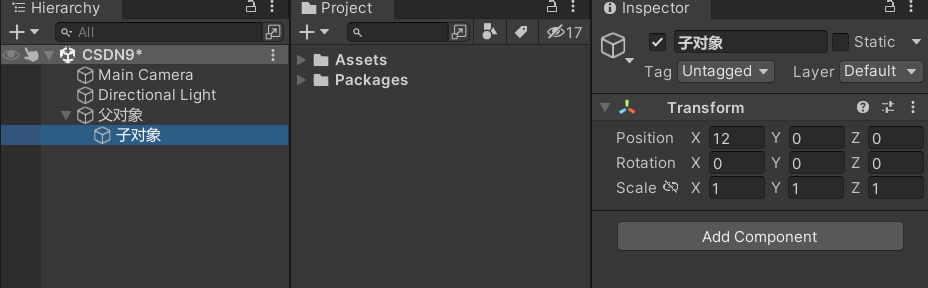
（4）实际的世界坐标位置：（17,5,5）= （12,0,0）+（5,5,5）

3、一些注意点

（1）不可单独修改坐标分量

        错误写法：

transform.position.x = 10; // 编译报错！Vector3是结构体，需整体修改

        正确方法： 

方法1：构造新Vector3，保留其他分量

transform.position = new Vector3(10, transform.position.y, transform.position.z);

方法2：先提取变量，再赋值

Vector3 pos = transform.position;pos.x = 10;transform.position = pos;

（2）对象的朝向属性

Transform提供了三个关键方向向量（世界空间方向）：和和上面的三维向量是一样的

transform.forward; // 对象正前方（Z轴正方向）transform.up; // 对象正上方（Y轴正方向）transform.right; // 对象右侧（X轴正方向）

作用：

        控制移动方向（如 transform.Translate(transform.forward * speed)）。

        计算物体间的相对方向（如炮口朝向目标）。

（3）父子层级的影响

修改父对象的 position 或 localPosition 会联动所有子对象的位置。

若需保持子对象的世界坐标不变，可先解除父子关系再修改。

小结：

世界坐标（position）用于全局定位，本地坐标（localPosition）用于相对父对象的局部定位。

操作坐标时需注意父子关系和分量修改的限制，灵活运用朝向属性可简化方向逻辑。

4、位移

        这是官方名词，说人话，可以理解为一段一段的位置偏移，例如当前位置是（0,0,0），我移动到了这一个点（1,1,1），这之间的距离，就是位移，是具有方向的。而在游戏中，如果你要进行位移，那肯定就是这么一段一段位移拼凑起来的，为了更加的丝滑，所以我们会×上帧间隔时间。所以得出位移的计算公式：

        最终位置 += 方向 × 帧时间间隔；

        关于上述公式的理解：因为方向就是一个小的和原来位置的偏移（这样理解，就是你在原位置上按照你想移动的方向，比如说上方，你就在自己的positon.y稍微加了一点点值，加完之后得到的新三维向量，即方向），然后×时间用于控制每一段的位移距离，因为你是会再Update里面执行这个函数语句的，如果不加以控制，那么就会飞起来！飞快。通过不断的累加，就达到了往一个方向移动的效果。同时为了控制移动的速率，我们可以添加一个移动速度，即：

        最终位置+=方向 × 移动速度 × 帧间隔时间

这就是在Unity中使得物体移动的基本原理：

接下来我们讲讲常用的两种实现方式：

方式一：手动计算并修改Position

        通过直接修改 transform.position 实现位移，默认基于世界坐标系。

例如：

// 沿世界坐标系Z轴正方向移动transform.position += Vector3.forward * 10 * Time.deltaTime;// 沿物体自身面朝向（世界坐标系中的方向）移动transform.position += transform.forward * 10 * Time.deltaTime;// 沿世界坐标系Y轴正方向移动（如上升）transform.position += Vector3.up * 10 * Time.deltaTime;

优劣：

优点：
直观，适合需要 精确控制世界坐标 的场景（如瞬移、固定路径移动）。

缺点：
代码较长，需手动处理方向逻辑。
若物体有父级，需额外计算本地坐标系方向。

方式二：使用Transform.Translate方法

        通过内置API Translate() 实现位移，默认基于自身坐标系，可指定参考坐标系。

基本语法：

// 参数1：移动方向与距离// 参数2（可选）：坐标系类型，默认为 Space.Self（自身坐标系）transform.Translate(Vector3.forward * 10 * Time.deltaTime, Space.World);

参数组合效果

方向向量 坐标系参数 实际移动方向 Vector3.forward Space.World 沿 世界坐标系Z轴正方向 移动 Vector3.forward Space.Self 沿 物体自身面朝向 移动（与旋转同步） transform.forward Space.World 沿 物体当前面朝向的世界坐标方向 移动 transform.forward Space.Self 等同于 Vector3.forward + Space.Self

 例如：

//1.相对于世界坐标系的 Z轴移动 始终是朝世界坐标系的Z轴正方向移动this.transform.Translate(Vector3.forward * 10 * Time.deltaTime,Space.World);//2.相对于世界坐标的 自己面朝向去运动 始终朝向自己的面朝向运动this.transform.Translate(this.transform.forward * 10 * Time.deltaTime, Space.World);//3.相对于自己坐标系下的 自己的面朝向向量去运动（一定不会让物体这样移动的） XXXthis.transform.Translate(this.transform.forward * 10 * Time.deltaTime, Space.Self);//4.相对于自己的坐标轴下的Z轴正方向移动 始终朝自己的面朝向移动this.transform.Translate(Vector3.forward * 10 * Time.deltaTime, Space.Self);

        一般我们都不会通过位移的方式去直接改变这个position,因为充满着不确定性。 

二、角度和旋转

        和位置一样，角度也分为世界坐标系角度和自身坐标系角度。这个角度很重要，后面还有一个四元数的知识，现在我们只简单讲讲面板上的这个角，即欧拉角：欧拉角就是用 三个角度（X、Y、Z轴）表示物体的旋转，类似飞机的 俯仰（点头）、偏航（摇头）、翻滚（侧身）

想象你是一个飞行员：
X轴旋转（俯仰）：飞机 上下点头（比如爬升或俯冲）。
Y轴旋转（偏航）：飞机 左右转头（比如改变飞行方向）。
Z轴旋转（翻滚）：飞机 侧身倾斜（比如空中特技翻滚）。

图示：

（1）我们创建三个用于演示不同角度变化的平面，其中不同的颜色代表等会改变那个方向上的角度

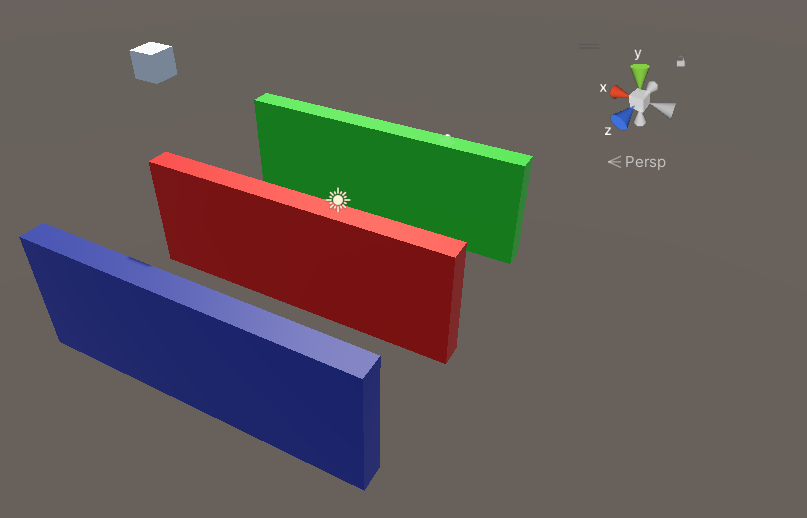
（2） 首先我们改变沿x轴方向的角度，可以看出实际上就是将于X轴不相关的另外两个轴组成的平面发生了旋转，围绕着X轴转。

（3）旋转另外两个轴的角度，黑色的是不作任何处理

         小结：沿着某一个方向旋转，即就是以这个方向作为一根轴，然后它作为一个平面的法向量，旋转这个平面，即沿着该方向旋转。

相关参数和使用方法：    

        角度获取与设置

1. 世界坐标系与本地坐标系角度

eulerAngles：
获取或设置物体 相对于世界坐标系 的欧拉角（绝对旋转）。
localEulerAngles：
获取或设置物体 相对于父对象坐标系 的欧拉角（本地旋转）。

// 获取世界坐标系下的角度Vector3 worldRotation = transform.eulerAngles;// 设置世界坐标系下的角度（绕Y轴旋转90度）transform.eulerAngles = new Vector3(0, 90, 0);// 获取本地坐标系下的角度Vector3 localRotation = transform.localEulerAngles;// 设置本地坐标系下的角度（绕Y轴旋转90度）transform.localEulerAngles = new Vector3(0, 90, 0);

        仍然值得我们注意的是，角度也是一个整体变量，是不能局部修改的，和位置一样。

        不可单独修改分量：与位置（Position）类似，欧拉角必须整体赋值： 

// 错误写法！transform.eulerAngles.y = 90; // 正确写法：构造新Vector3Vector3 newRotation = transform.eulerAngles;newRotation.y = 90;transform.eulerAngles = newRotation;

父子关系影响：

若物体无父级，eulerAngles 和 localEulerAngles 值相同。
若父级有旋转，修改 localEulerAngles 会叠加父级旋转效果。 

       2. 旋转的两种实现方式：这里和位置是及其类似的，所以不再解释原理，直接上方法！不过值得注意的是，我们在这里不会选择自己手动实现通过改变面板上数值的方式旋转，而是通过API

1. 自转：Rotate 方法

        通过 Rotate 实现物体绕某个轴的持续旋转，支持 自身坐标系 或 世界坐标系。

方式一：指定旋转向量

自转每个轴 具体转多少度第一个参数 相当于是旋转的角度 每一帧第二个参数默认不填 就是相当于自己坐标系 进行旋转// 绕自身Y轴旋转（每帧旋转1度）transform.Rotate(Vector3.up * Time.deltaTime * 10);// 绕世界Y轴旋转（需显式指定坐标系）transform.Rotate(Vector3.up * Time.deltaTime * 10, Space.World);

方式二：指定轴和角度

相对于某个轴转多少度参数一：是相对于哪个轴进行转动参数二：是转动的角度是多少参数三：默认不填 就是相对于自己坐标系 进行旋转 如果填Space.World 就是相对于世界坐标系进行旋转// 绕自身Y轴旋转transform.Rotate(Vector3.up, 10 * Time.deltaTime);// 绕世界Y轴旋转transform.Rotate(Vector3.up, 10 * Time.deltaTime, Space.World);

2. 绕点旋转：RotateAround 方法

        使物体绕场景中某个点（如原点、其他物体位置）旋转，常用于行星绕太阳运动、摄像机环绕目标等场景。

相对于某一个点进行旋转参数一：是相对于哪个点进行旋转参数二：相对于那一个点的哪个轴参数三：旋转的角度// 绕世界原点（0,0,0）的Y轴旋转（每帧10度）transform.RotateAround(Vector3.zero, Vector3.up, 10 * Time.deltaTime);// 绕目标物体位置旋转Vector3 targetPos = target.transform.position;transform.RotateAround(targetPos, Vector3.up, 10 * Time.deltaTime);

一些注意事项：

①角度跳跃问题：
直接修改 eulerAngles 可能导致角度从359°跳转到0°，需用插值（Mathf.LerpAngle）平滑过渡。
②万向节锁（Gimbal Lock）：
欧拉角在特定角度（如X轴90度）会丢失一个旋转自由度，复杂旋转建议使用四元数（Quaternion）。 

        可能会有人会疑问？那那那你这个不是一直在移动，在旋转，你咋停捏。这个不急，这个是后话，后面会使用一个插值函数，平滑过渡到某一个位置或者角度

三、缩放和看向

缩放：

图中标红的部分，就是可以整体控制三个维度的数值

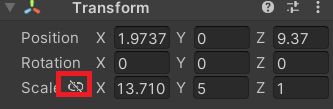
未改变

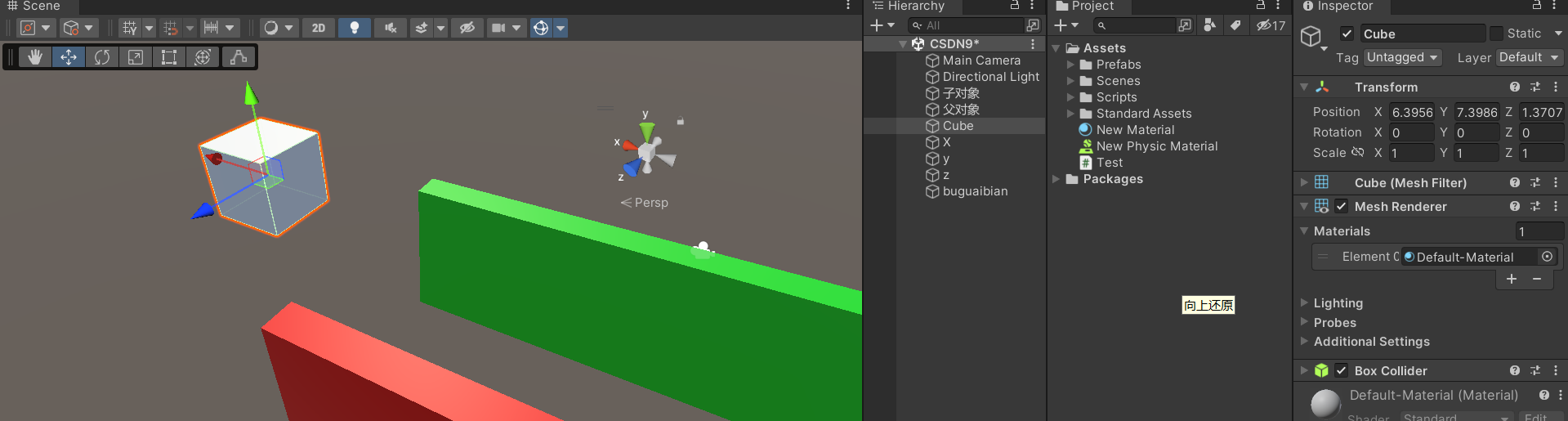
呵长大了

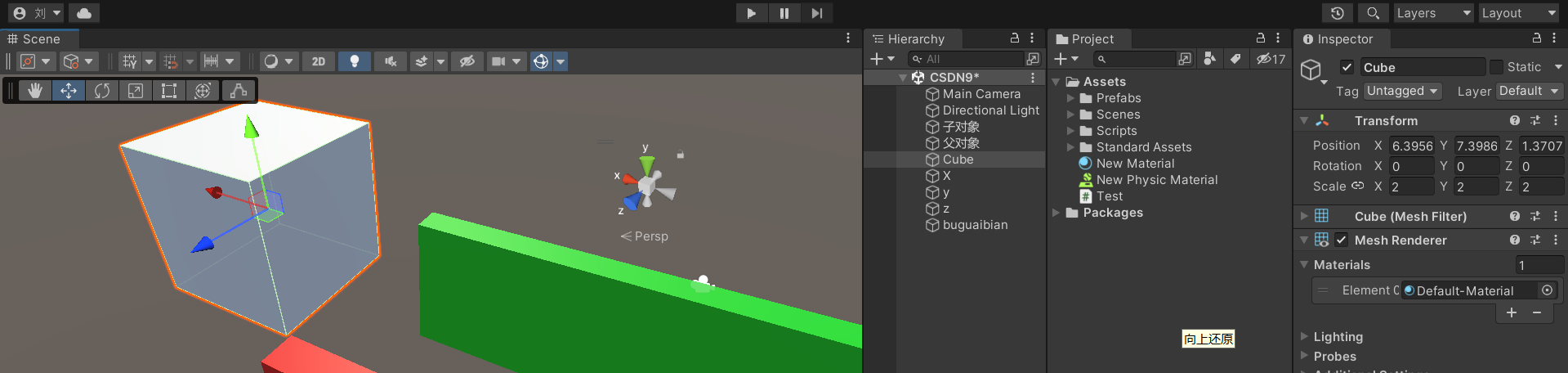这个参数就很简单，直接这么改变就是了。

总结一下：

lossyScale​：

        表示对象相对于世界坐标系的缩放值（只读属性）。若对象有父物体，其值会受父物体缩放的影响。无法直接修改。

localScale​：

        表示对象相对于父物体坐标系的缩放值（可读写）。直接修改此属性可调整对象的本地缩放。

示例一下：

print(transform.lossyScale); // 输出世界坐标系的缩放transform.localScale = new Vector3(3, 3, 3); // 设置本地缩放为3倍

 注意一下：

​无直接缩放API​：

        Unity未提供类似Translate或Rotate的缩放方法，需手动计算并赋值给localScale。

​缩放继承性​：

        父物体的缩放会影响子物体的世界缩放（lossyScale）。若需精准控制世界缩放，需调整层级结构。

​非均匀缩放问题​：

        非均匀缩放（如x、y、z不同）可能导致碰撞体形状异常或物理模拟不准确。

看向：顾名思义就是看向一个地方，一般是看向一个点。或者一个对象，这个很简单。有一个API提供给我们使用。

//让一个对象的面朝向 可以一直看向某一个点或者某一个对象//看向一个点this.transform.LookAt(new Vector3(0,0,0));//相对于世界坐标系//看向一个对象this.transform.LookAt(cube.transform);//相对于世界坐标系

//小结
//缩放相关
//相对于世界坐标系的缩放 只能得 不能改
//只能去修改相对于本地坐标系的缩放（相对于父对象）
//没有提供对应的API来进行 缩放变化 只有自己算
//看向 
//LookAt
//看向一个点
//看向一个对象
//一定记住 只有写在Update里 才会每帧执行

四、父子关系

        在前面我们也学习了一个关于父子关系。这里也有一个在Transform中的父子关系。前面的更加的基类，这里相当于是扩展补充。

        父子关系基础操作

1. 获取与设置父对象

获取父对象：

Transform parent = transform.parent; // 若无父对象返回null

设置父对象：

// 直接赋值transform.parent = newParent; // 使用API（推荐）transform.SetParent(newParent, true); 

参数 worldPositionStays：
true：子对象保留当前世界坐标，重新计算本地坐标。
false：直接将世界坐标复制为本地坐标（可能导致位置突变）。

2. 解除父子关系

解除单个子对象：

child.parent = null; // 子对象成为独立根对象

解除所有子对象：

transform.DetachChildren(); // \"抛妻弃子\"，子对象保留当前世界坐标

        子对象操作

1. 获取子对象

按名称查找：

Transform child = transform.Find(\"子对象名\"); // 特点：仅查找直接子对象，可找到失活对象

遍历子对象：注意 是找不到自己子对象的子对象的

for (int i = 0; i < transform.childCount; i++) { Transform child = transform.GetChild(i); // 按索引获取}

2. 子对象顺序管理

获取与设置顺序：

int index = child.GetSiblingIndex(); // 当前在所有孩子中的顺序编号child.SetAsFirstSibling(); // 置顶child.SetAsLastSibling();  // 置底child.SetSiblingIndex(2);  // 设为指定编号（越界则置底）

判断父子关系： 

bool isChild = child.IsChildOf(parent); // 是否为直接或间接子对象

Unity父子关系操作汇总表

---

父子关系基础操作

操作 方法/属性 说明 注意事项 获取父对象 transform.parent 返回父对象的Transform，若无父对象则返回 null。 若对象是根节点，parent 为 null。 设置父对象 transform.parent = newParent 直接修改父子关系，新父对象为 newParent。 可能导致子对象坐标突变（取决于父对象当前状态）。 API设置父对象 transform.SetParent(newParent, worldPositionStays) 参数1：新父对象；参数2：是否保留世界坐标。 worldPositionStays=true：重新计算本地坐标；false：直接复制世界坐标为本地坐标。 解除单个子对象 child.parent = null 解除指定子对象的父子关系，子对象成为独立根对象。 子对象的世界坐标保持不变。 解除所有子对象 transform.DetachChildren() 解除所有子对象的父子关系，子对象保留当前世界坐标。 常用于动态清空父对象下的所有子对象。

---

子对象操作

操作 方法/属性 说明 注意事项 按名称查找子对象 transform.Find(\"子对象名\") 查找直接子对象（仅限一级子对象）。 1. 可找到失活（Inactive）的子对象。
2. 无法查找孙子对象。 获取子对象总数 transform.childCount 返回直接子对象的数量（包含失活对象）。 不包含孙子对象。 按索引获取子对象 transform.GetChild(index) 通过索引获取子对象，索引范围 0 到 childCount-1。 索引越界会触发错误，需先检查 index < childCount。 遍历所有子对象 for (int i=0; i<childCount; i++){ GetChild(i) } 遍历直接子对象。 循环中避免动态增删子对象，否则可能引发索引错乱。 获取子对象顺序编号 child.GetSiblingIndex() 返回子对象在父级中的顺序编号（从0开始）。 编号反映在Hierarchy面板中的显示顺序。 设置子对象顺序 child.SetAsFirstSibling()
child.SetAsLastSibling()
child.SetSiblingIndex(n) 调整子对象在父级中的顺序：置顶、置底或指定位置。 SetSiblingIndex 超出范围时，子对象会被置底。 判断父子关系 child.IsChildOf(parent) 判断子对象是否直接或间接属于某个父对象。 可以检测多层嵌套的父子关系（如祖父-父-子）。

五、坐标转换

        就两点，世界转本地，本地转世界。

世界坐标转本地坐标

1. ​点的转换：InverseTransformPoint

​功能​：将世界坐标系的点 转换为相对于本地坐标系的点

​受缩放影响​：是（考虑父物体的缩放）。

Vector3 localPoint = transform.InverseTransformPoint(Vector3.forward);// 结果会受到物体位置、旋转和缩放的影响

2. ​方向的转换：InverseTransformDirection​

​功能​：世界坐标系的方向 转换为 相对于本地坐标系的方向
           可以理解为换了个坐标原点 重新计算各个坐标的位置
           计算的都是相对的 因为你自己的坐标原点也是在不断的相对于世界坐标系在不断的改变

​受缩放影响​：否（仅旋转）。

Vector3 localDir = transform.InverseTransformDirection(Vector3.forward);// 结果仅受物体旋转影响，与缩放无关

3. ​向量的转换：InverseTransformVector

​功能​：将世界坐标系的向量转换为本地坐标系的向量。相当于是直接把方向向量平移过去                 然后算现在的各分量

​受缩放影响​：是（考虑父物体的缩放）。

Vector3 localVector = transform.InverseTransformVector(Vector3.forward);// 结果受物体旋转和缩放影响，但不受位置影响

本地坐标转世界坐标

1. ​点的转换：TransformPoint​

​功能​：将本地坐标系的点转换为世界坐标系的点。和前面一样，就相当于是换了一个参考的坐标原点

​受缩放影响​：是。

Vector3 worldPoint = transform.TransformPoint(Vector3.forward);// 用于计算子物体在世界空间中的位置

2. ​方向的转换：TransformDirection​

​功能​：将本地坐标系的方向转换为世界坐标系的方向。

​受缩放影响​：否（仅旋转）。

Vector3 worldDir = transform.TransformDirection(Vector3.forward);// 常用于子弹发射方向（本地前方向转换为世界方向）

3. ​向量的转换：TransformVector​

​功能​：将本地坐标系的向量转换为世界坐标系的向量。

​受缩放影响​：是。

Vector3 worldDir = transform.TransformDirection(Vector3.forward);// 常用于子弹发射方向（本地前方向转换为世界方向）

 小结：

        前三个是世界转本地，后面是本地转世界。可以这样记忆，本地转世界比较的自然，于是没有翻转所哟不用Inverse

方法 输入类型 受缩放影响 典型应用场景 InverseTransformPoint 点 是 计算敌人相对于玩家的位置 InverseTransformDirection 方向 否 判断目标在物体的左侧或右侧 InverseTransformVector 向量 是 物理引擎中的相对力 TransformPoint 点 是 子物体在世界空间中的位置 TransformDirection 方向 否 发射子弹的方向 TransformVector 向量 是 施加本地坐标系定义的力

六、总结

位置（Position）

方法/属性 输入类型 描述 受缩放影响 典型应用场景 transform.position Vector3（世界坐标） 获取或设置物体的世界坐标系位置。 是 全局定位、瞬移 transform.localPosition Vector3（本地坐标） 获取或设置物体相对于父对象的本地坐标系位置。 是 父子结构中的局部定位 transform.Translate Vector3 + Space 按指定方向和坐标系移动物体（默认基于自身坐标系）。 是 角色移动、连续位移

---

位移（Movement）

方法 输入类型 描述 受缩放影响 典型应用场景 手动修改position Vector3 直接累加位移向量（如 position += forward * speed）。 是 精确控制位移方向 transform.Translate Vector3 + Space 按方向向量移动物体，支持世界/本地坐标系。 是 角色控制器、物理无关的简单移动

---

角度与旋转（Rotation）

方法/属性 输入类型 描述 受缩放影响 典型应用场景 transform.eulerAngles Vector3（世界欧拉角） 获取或设置物体的世界坐标系欧拉角。 否 全局朝向控制 transform.localEulerAngles Vector3（本地欧拉角） 获取或设置物体相对于父对象的本地欧拉角。 否 父子结构中的局部旋转 transform.Rotate Vector3 + Space 绕指定轴旋转固定角度，支持世界/本地坐标系。 否 自转（如旋转道具） transform.RotateAround Vector3（中心点）+ Vector3（轴） 绕场景中某一点旋转。 否 行星绕太阳运动、摄像机环绕目标 transform.LookAt Vector3或Transform 让物体面朝指定点或对象。 否 摄像机聚焦、敌人锁定玩家

---

缩放（Scale）

方法/属性 输入类型 描述 受缩放影响 典型应用场景 transform.localScale Vector3（本地缩放） 获取或设置物体相对于父对象的本地缩放。 是 父子结构中的尺寸调整 transform.lossyScale Vector3（世界缩放） 获取物体在世界坐标系下的实际缩放（只读）。 - 计算物体实际尺寸

---

父子关系（Parenting）

方法/属性 输入类型 描述 典型应用场景 transform.parent Transform或null 获取或设置父对象，直接修改父子关系。 动态挂载子对象（如装备武器） transform.SetParent Transform + bool 设置父对象并选择是否保留世界坐标（worldPositionStays）。 精确控制父子坐标继承 transform.DetachChildren 无 解除所有子对象的父子关系。 清空父对象下的子对象 transform.Find string（子对象名） 按名称查找直接子对象（不支持孙子对象）。 快速获取特定子对象 transform.GetChild int（索引） 通过索引获取子对象（索引范围：0到childCount-1）。 遍历子对象 transform.childCount 无 获取直接子对象数量（包含失活对象）。 统计子对象数量 child.IsChildOf Transform（父对象） 判断子对象是否属于某个父对象（支持多层嵌套）。 验证层级关系

---

坐标转换（Space Conversion）

方法 输入类型 描述 受缩放影响 典型应用场景 TransformPoint Vector3（本地坐标） 将本地坐标转换为世界坐标。 是 计算子物体在世界空间中的实际位置 InverseTransformPoint Vector3（世界坐标） 将世界坐标转换为本地坐标。 是 小地图中显示敌人相对位置 TransformDirection Vector3（本地方向） 将本地方向转换为世界方向（仅方向，无缩放影响）。 否 发射子弹方向控制 InverseTransformDirection Vector3（世界方向） 将世界方向转换为本地方向（仅方向）。 否 判断目标在物体的左侧/右侧 TransformVector Vector3（本地向量） 将本地向量转换为世界向量（含缩放影响）。 是 施加本地坐标系定义的力 InverseTransformVector Vector3（世界向量） 将世界向量转换为本地向量（含缩放影响）。 是 物理引擎中的相对力计算