【AI大模型入门指南】数学基础（概率论）看不懂？这篇保姆级精讲！_大模型概率

一、概率与统计（Probability and Statistics）

概率论和统计学在深度学习中至关重要。概率论为模型的不确定性和预测提供理论基础。数据位置和数据散布的概念帮助我们理解和描述数据的中心趋势和变异性。图形表示技术，如直方图和散点图，用于数据的可视化和探索。离散型概率分布和连续型概率分布则用于描述不同类型的数据和其分布模式。

在统计学中，点估计和区间估计用于推断数据的参数，从而帮助我们理解模型的预测准确性和置信区间。假设性检验用于评估模型假设的有效性和显著性，确保结果的可靠性。相关性分析则用于发现变量之间的关系和依赖性，从而帮助我们优化模型和提升性能。通过概率论和统计学工具，深度学习能够更好地处理数据的不确定性、进行模型评估和优化，提升预测的准确性和可靠性。

如果你正在开始学习深度学习，我这边经过上百次修改整理出了一套深度学习机器学习的入门学习路线图，能够帮你最大效率的学习深度学习，少走弯路！。

    如果你需要学习路线的pdf可以直接扫码添加我的助手让她无偿及时分享给大家！

二、 概率论

---

1. 数据位置

平均数（Average）是表示一组数据集中趋势的量数，是指在一组数据中所有数据之和再除以这组数据的个数，是反映数据集中趋势的一项指标。
特点：

• （1）易受极端值影响。

• （2）数学性质优良。

• （3）数据对称分布或接近对称分布时应用。

众数（Mode）是指在统计分布上具有明显集中趋势点的数值，代表数据的一般水平。 也是一组数据中出现次数最多的数值，有时众数在一组数中有好几个，用M表示。
特点：

• （1）组数据中出现次数最多的变量值。

• （2）适合于数据量较多时使用。

• （3）不受极端值的影响。

• （4）一组数据可能没有众数也可能有几个众数。

中位数（Median）又称中值，统计学中的专有名词，是按顺序排列的一组数据中居于中间位置的数，代表一个样本、种群或概率分布中的一个数值，其可将数值集合划分为相等的上下两部分。对于有限的数集，可以通过把所有观察值高低排序后找出正中间的一个作为中位数。如果观察值有偶数个，通常取最中间的两个数值的平均数作为中位数。
特点：

• （1）不受极端值的影响。在有极端数值出现时，中位数作为分析现象中集中趋势的数值，比平均数更具有代表性。

• （2）主要用于顺序数据，也可以用于数值型数据，但不能用于分类数据。

• （3）各变量值与中位数的离差绝对值之和最小。

四分位数（Quartile）也称四分位点，是指在统计学中把所有数值由小到大排列并分成四等份，处于三个分割点位置的数值就是四分位数。四分位数多应用于统计学中的箱线图绘制。它是一组数据排序后处于25%和75%位置上的值。四分位数是通过3个点将全部数据等分为4部分，其中每部分包含25%的数据。很显然，中间的四分位数就是中位数，因此通常所说的四分位数是指处在25%位置上的数值（称为下四分位数）和处在75%位置上的数值（称为上四分位数）。与中位数的计算方法类似，根据未分组数据计算四分位数时，首先对数据进行排序，然后确定四分位数所在的位置，该位置上的数值就是四分位数。

 这份完整版的大模型 AI 学习资料已经上传CSDN，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】

假设我们有以下一组数据:

对于奇数个数据，中位数是第

个数据。
这里数据个数

，所以中位数位置是第

个数据。所以中位数

是第 6 个数据，也就是 41 。

下四分位数是位于第

个数据。
这里数据个数

 ，所以下四分位数位置是第

个数据。
所以下四分位数

 是第 3 个数据，也就是 36 。

上四分位数是位于第

个数据。
这里数据个数

 ，所以上四分位数位置是第

个数据。所以上四分位数

是第 9 个数据，也就是 44 。

2. 数据散布

---

数学期望

数学期望（Mathematical expectations）是对长期价值的数字化衡量。

数学期望值是理想状态下得到的实验结果的平均值，是试验中每次可能的结果概率乘以其结果的总和，是最基本的数学特征之一，它反映随机变量平均取值的大小。换句话说，期望值像是随机试验在同样的机会下重复多次，所有那些可能状态的平均结果。

• 离散型随机变量数学期望严格的定义为: 设离散型随机变量

  

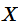
  的分布列为

  

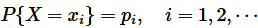
  。若级数

  

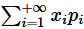
  绝对收敛, 则称级数

  

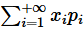
   的和为随机变量

  

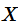
  的数学期望(也称期望或均值), 记为

  

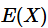
  。即

  

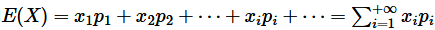
• 连续型随机变量数学期望严格的定义为: 设连续型随机变量

  

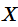
  的概率密度函数为

  

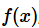
  ,积分

  

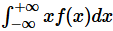
  绝对收敛, 则定义

  

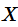
  的数学期望

  

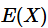
  为

  

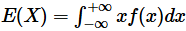
一个随机变量的数学期望是一个常数，它表示随机变量取值的一个平均；这里用的不是算术平均，而是以概率为权重的加权平均。数学期望反映了随机变量的一大特征，即随机变量的取值将集中在其期望值附近，这类似于物理中质点组成的质心。

最后，强调一下平均数和数学期望的联系：平均数是一个统计学概念，期望是一个概率论概念。平均数是实验后根据实际结果统计得到的样本的平均值，期望是实验前根据概率分布“预测”的样本的平均值。之所以说“预测”是因为在实验前能得到的期望与实际实验得到的样本的平均数总会不可避免地存在偏差，毕竟随机实验的结果永远充满着不确定性。期望就是平均数随样本趋于无穷的极限。

方差

方差（Variance）用来描述随机变量与数学期望的偏离程度。

如果把单个数据点称为“ 

 ”, 那么 “ 

 ” 是第一个值, “ 

 ” 是第二个值, 以此类推, 一共有

个值。均值称为 “

 ”。

• 初看上去

  

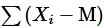
  就可以作为描述数据点散布情况的指标, 也就是把每个

   

  

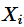
  与

  

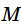
  的偏差求和。换句话讲，是单个数据点减去数据点的平均的总和。

  • 此方法看上去很有逻辑性，但却有一个致命的缺点：高出均值的值和低于均值可以相互抵消，因此上述定义的结果趋近于0。

  • 这个问题可以通过取差值的绝对值来解决（也就是说，忽略负值的符号），但是由于各种原因，统计学家不喜欢绝对值。另外一个剔除负号的方法是取平方，因为任何数的平方肯定是正的，因此便得到了方差的分子

    

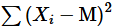
• 再考虑一个问题: 比如有 25 个值的样本, 根据方差计算出标准差是 10 。如果把这 25 个值复制一下变成 50 个样本呢, 直觉上 50 个样本的数据点分布情况应该不变的, 但是公式中的累加会产生更大的方差值。

  • 所以需要通过除以数据点数量 n 来弥补这个漏洞。

因此, 方差的定义如下:

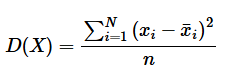
标准差

标准差（standard deviation）是通过方差除以样本量再开根号得到的，具体公式如下：

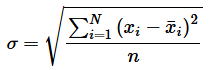
与方差的作用类似, 标准差也能反映一个数据集的离散程度, 它是各点与均值的平均距离。平均数相同的数据, 标准差未必相同。

极差

极差又称范围误差或全距(Range)，以R表示，计算方法是其最大值与最小值之间的差距，即最大值减最小值后所得数据。

四分数范围

四分位数，即把所有数值由小到大排列并分成四等份，处于三个分割点位置的数值就是四分位数。第三四分位数与第一四分位数的差值称为四分位数间距（Interquartile Range，IQR），简称四分位距。
四分位距是描述统计学中的一种方法，但由于四分位距不受极大值或极小值的影响，常用于描述非正态分布资料的离散程度，其数值越大，数据离散程度越大，反之离散程度越小。

3. 图形表示

---

常见的数据图形化表示方式有很多，每种方式都适用于展示不同类型的数据和揭示不同的关系。以下是几种常见的数据图形化表示方式：

• 柱状图（Bar Chart）：用于比较不同类别的数据值。

• 折线图（Line Chart）：用于展示数据随时间的变化趋势。

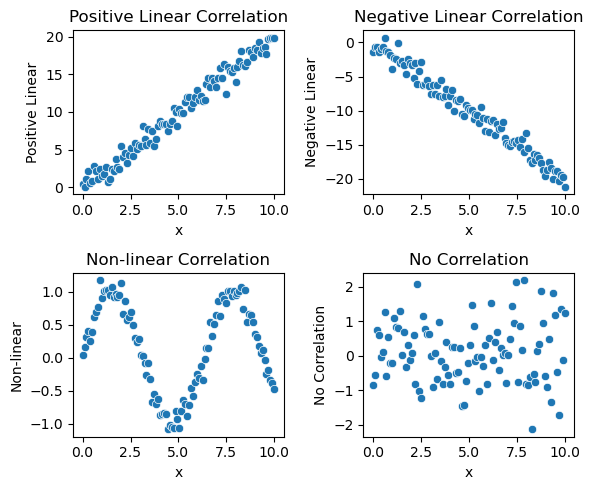
• 散点图（Scatter Plot）：用于展示两个变量之间的关系。

• 饼图（Pie Chart）：用于展示数据在一个整体中的占比。

• 箱线图（Box Plot）：用于展示数据的分布及其异常值，尤其适合展示四分位数。

• 直方图（Histogram）：用于展示数据的频率分布。

• 热图（Heatmap）：用于展示数值变量的密度分布。

• 雷达图（Radar Chart）：用于展示多变量数据的比较。

每种图形化表示方式都有其独特的用途和优势，选择适合的图表类型可以更清晰地传达数据的含义。

import numpy as npimport pandas as pdfrom scipy import statsfrom sklearn.datasets import load_iris# Load the Iris datasetiris = load_iris()df = pd.DataFrame(data=iris.data, columns=iris.feature_names)# Calculate statisticsstatistics = {}for column in df.columns:    data = df[column]    statistics[column] = {        \'mean\': np.mean(data),        \'mode\': stats.mode(data, keepdims=True)[0][0],        \'median\': np.median(data),        \'quartiles\': np.percentile(data, [25, 50, 75]),        \'variance\': np.var(data),        \'standard_deviation\': np.std(data),        \'range\': np.ptp(data),        \'interquartile_range\': stats.iqr(data)    }# Convert statistics to DataFrame for better visualizationstats_df = pd.DataFrame(statistics).Tstats_df

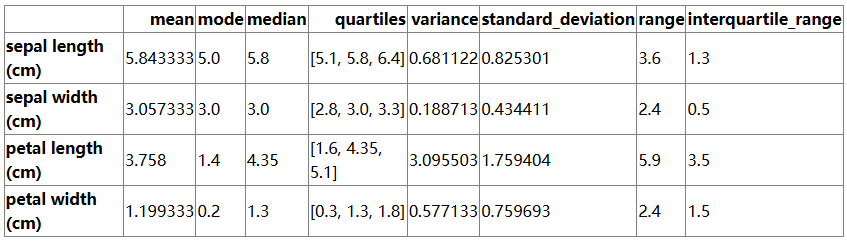
import matplotlib.pyplot as pltimport seaborn as snsimport numpy as npimport pandas as pdfrom sklearn import datasets# Load the iris datasetiris = datasets.load_iris()df = pd.DataFrame(iris.data, columns=iris.feature_names)df[\'species\'] = iris.target# Plotting all charts as subplots in a single figurefig, axes = plt.subplots(4, 2, figsize=(10, 15), subplot_kw=dict(polar=False))# Bar Chartsns.barplot(x=\'species\', y=\'sepal length (cm)\', data=df, ax=axes[0, 0])axes[0, 0].set_title(\'Mean Sepal Length by Species\')axes[0, 0].set_xlabel(\'Species\')axes[0, 0].set_ylabel(\'Sepal Length (cm)\')# Line Chartaxes[0, 1].plot(df[\'sepal length (cm)\'])axes[0, 1].set_title(\'Trend of Sepal Length Across Samples\')axes[0, 1].set_xlabel(\'Sample Index\')axes[0, 1].set_ylabel(\'Sepal Length (cm)\')# Scatter Plotsns.scatterplot(x=\'sepal length (cm)\', y=\'petal length (cm)\', hue=\'species\', data=df, ax=axes[1, 0])axes[1, 0].set_title(\'Relationship Between Sepal Length and Petal Length\')axes[1, 0].set_xlabel(\'Sepal Length (cm)\')axes[1, 0].set_ylabel(\'Petal Length (cm)\')# Pie Chartspecies_counts = df[\'species\'].value_counts()axes[1, 1].pie(species_counts, labels=iris.target_names, autopct=\'%1.1f%%\', startangle=140)axes[1, 1].set_title(\'Proportion of Each Species\')# Box Plotsns.boxplot(x=\'species\', y=\'sepal length (cm)\', data=df, ax=axes[2, 0])axes[2, 0].set_title(\'Distribution of Sepal Length by Species\')axes[2, 0].set_xlabel(\'Species\')axes[2, 0].set_ylabel(\'Sepal Length (cm)\')# Histogramaxes[2, 1].hist(df[\'sepal length (cm)\'], bins=20, edgecolor=\'k\')axes[2, 1].set_title(\'Frequency Distribution of Sepal Length\')axes[2, 1].set_xlabel(\'Sepal Length (cm)\')axes[2, 1].set_ylabel(\'Frequency\')# Heatmapsns.heatmap(df.iloc[:, :-1].corr(), annot=True, cmap=\'coolwarm\', vmin=-1, vmax=1, ax=axes[3, 0])axes[3, 0].set_title(\'Heatmap of Feature Correlations\')# Radar Chart# Create a subplot with polar coordinates for the radar chartax_radar = fig.add_subplot(4, 2, 8, polar=True)# Calculate mean values for each speciesmean_values = df.groupby(\'species\').mean()categories = list(mean_values.columns)values = mean_values.values# Number of variablesnum_vars = len(categories)# Compute angle for each axisangles = np.linspace(0, 2 * np.pi, num_vars, endpoint=False).tolist()angles += angles[:1]# Plot data on the radar chartfor i, value in enumerate(values):    data = np.append(value, value[0])    ax_radar.plot(angles, data, linewidth=2, linestyle=\'solid\', label=iris.target_names[i])    ax_radar.fill(angles, data, alpha=0.25)# Set the axis labelsax_radar.set_yticklabels([])ax_radar.set_xticks(angles[:-1])ax_radar.set_xticklabels(categories)# Add title and legendax_radar.set_title(\'Radar Chart of Mean Feature Values by Species\')ax_radar.legend(loc=\'upper right\', bbox_to_anchor=(1.3, 0))plt.tight_layout()plt.show()

 离散型概率分布

---

离散数据即数据的取值是不连续的。例如掷硬币就是一个典型的离散数据，因为抛硬币只有2种数值（也就是2种结果，要么是正面，要么是反面）。概率分布清楚而完整地表示了随机变量 X 所取值的概率分布情况。离散型随机变量的概率分布可用表格形式来表示, 称之为分布列, 见下表。

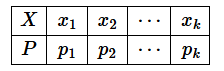
离散型随机变量的概率分布列具有下列性质：

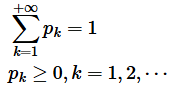
那么为什么要去统计概率分布呢？当统计学家们开始研究概率分布时，他们看到，有几种形状反复出现，于是就研究它们的规律，根据这些规律来解决特定条件下的问题。大家想想当年高考的时候，为了备战语文作文，可以准备一个自己的“万能模板”，任何作文题目都可以套用该模板，快速解决作文这个难题。同样的，记住概率里这些特殊分布的好处就是：下次遇到类似的问题，就可以直接套用“模板”（这些特殊分布的规律）来解决问题了。而这就是研究概率分布的意义所在。

两点分布

如果随机变量

的分布列如下:

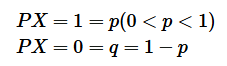
则称

 服从两点分布。两点分布也叫伯努利分布（Bernoulli）或 0-1 分布。
两点分布虽简单但很有用。当随机试验只有 2 个可能结果, 且都有正概率时, 就确定一个服从两点分布的随机变量。例如检查产品质量是否合格; 检查某车间的电力消耗是否超过负荷; 某射手对目标的一次射击是否中靶等试验都可以用服从二点分布的随机变量来描述。

二项分布

如果随机变量

的概率分布为:

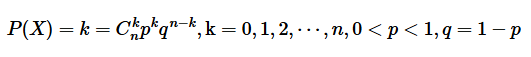
则称

服从参数为

的二项分布。其中, 二项定理的系数计算方法如下:

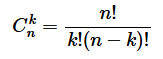
二项分布记为

或

。

• 服从二项分布的随机变量的直观背景可解释为:

  • 重复服从二项分布的实验

    

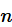
    次, 某事件

    

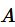
    发生的次数

    

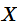
    是服从二项分布的随机变量。

• 二项分布有什么用呢？

  • 假设遇到一个事情，如果该事情发生次数固定，而想要统计的是成功的次数，那么就可以用二项分布的公式快速计算出概率来。

• 如何判断是不是二项分布？

  • 顾名思义，二项代表事件有2种可能的结果，把一种称为成功；另外一种称为失败。

  • 生活中有很多这样2种结果的二项情况，例如表白结果是二项的，一种成功；另一种是失败。

• 二项分布符合下面4个特点：

  • 做某件事的次数（也叫试验次数）是固定的，用n表示。

  • 每一次事件都有两个可能的结果（成功，或者失败）。

  • 每一次成功的概率都是相等的，成功的概率p用表示

  • 感兴趣的是成功x次的概率是多少。

• 二项分布的期望

  • 

• • 表示某事情发生

    

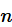
    次, 预期成功多少次。

那么知道这个期望有什么用呢?

做任何事情之前, 知道预期结果肯定会对后面的决策有帮助。比如拋硬币 5 次, 每次概率是

, 那么期望

次, 也就是有大约 3 次可以抛出正面。

再比如投资了 5 支股票，假设每支股票赚到钱的概率是80%, 那么期望 

, 也就是预期会有 4 只股票投资成功赚到钱。

几何分布

几何分布实际上与二项分布非常的像，先来看几何分布的4个特点：

1. 做某件事的次数（也叫试验次数）是固定的，用n表示。

2. 每一次事件都有两个可能的结果（成功，或者失败）。

3. 每一次成功的概率都是相等的，成功的概率p用表示

4. 感兴趣的是进行次尝试这个事情，取得第1次成功的概率是多大。
   正如读者所看到的，几何分布和二项分布的区别只有第4点，也就是解决问题目的不同。几何分布的数学公式如下：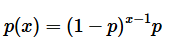

   

其中

为成功概率, 即为了在第

次尝试取得第 1 次成功, 首先要失败

 次。

继续刚才的例子，假如在表白之前, 计算出即使尝试表白 3 次, 在最后 1 次成功的概率还是小于 50%,还没有抛硬币的概率高。那就要考虑换个追求对象。或者首先提升下自己, 提高自己每一次表白的概率。

最后, 几何分布的期望是

 。假如每次表白的成功概率是 60%, 同时也符合几何分布的特点, 所以期望

。这意味着表白 1.67 次（约等于 2 次）会成功。

泊松分布

如果随机变量

的概率分布为：

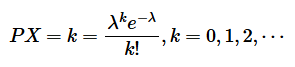
其中常数

, 则称

服从参数为

的泊松分布, 记为

 。 

代表事情发生的次数,

代表给定时间范围内事情发生的平均次数。

• 那么泊松分布有什么用？

  • 如果想知道某个时间范围内，发生某件事情

    

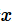
    次的概率是多大。这时候就可以用泊松分布轻松搞定。

  • 比如一天内中奖的次数，一个月内某机器损坏的次数等。

• 知道这些事情的概率有什么用呢？
  *当然是根据概率的大小来做出决策了。比如组织一次抽奖活动，最后算出来一天内中奖10次的概率都超过了90%，然后进行期望和活动成本的比较，发现要赔不少钱，那这个活动就别组织了。

泊松分布符合以下3个特点：

1. 事件是独立事件。

2. 在任意相同的时间范围内，事件发的概率相同。

3. 想知道某个时间范围内，发生某件事情次的概率是多大。

例如组织了一个促销抽奖活动, 只知道 1 天内中奖的平均个数为 4 个, 想知道 1 天内恰巧中奖次数为 8 的概率是多少?

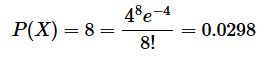
泊松概率还有一个重要性质，它的数学期望和方差相等，都等于

。

离散型数据分布小结

• 二点分布: 表示一次试验只有两种结果即随机变量

  

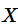
  只有两个可能的取值。

• 二项分布: 感兴趣的是成功

  

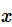
  次的概率是多少。

• 几何分布: 感兴趣的是进行

  

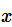
  次尝试这个事情, 取得第 1 次成功的概率是多大。

• 泊松分布: 想知道某个范围内, 发生某件事情

  

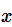
  次的概率是多大。

 连续型概率分布

---

概率密度函数

对于连续型随机变量，由于其取值不能一一列举出来，因而不能用离散型随机变量的分布列来描述其取值的概率分布情况。但人们在大量的社会实践中发现连续型随机变量落在任一区间

上的概率, 可用某一函数

在

上的定积分来计算。于是有下列定义:对于随机变量

, 如果存在非负可积函数

, 使对任意

都有

。则称

为连续型随机变量, 并称

为连续型随机变量X 的概率密度函数（Probability Density Function, PDF），简称概率密度或密度函数。

累积分布函数

不管

是什么类型（连续/离散/其他）的随机变量, 都可以定义它的累积分布函数 

(cumulative distribution function, CDF), 有时简称为分布函数。对于连续性随机变量, CDF 就是 PDF 的积分, PDF 就是 CDF 的导数:

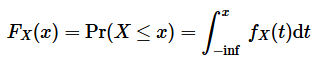
均匀（uniform）分布

设连续型随机变量

在有限区间

 上取值, 且它的概率密度为:

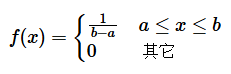
则称

服从区间

上的均匀分布, 可记成

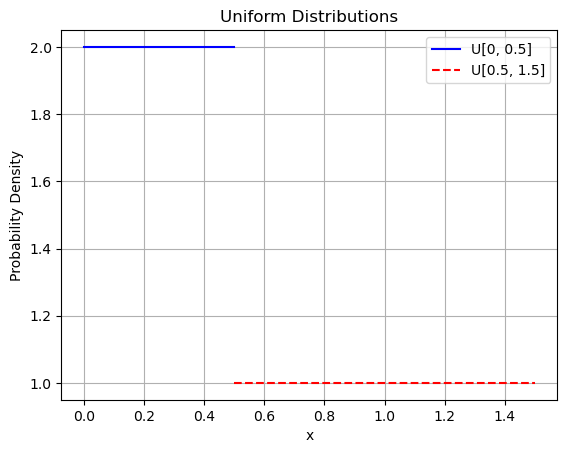
, 如图 1-32 所示。其中第一种分布使用实线表示, 范围为

, 概率密度为 2 ; 第二种分布使用虚线表示, 范围为

,概率密度为 1 。​​​​​​​

import numpy as npimport matplotlib.pyplot as plt# Define the ranges for the two distributionsx1 = np.linspace(0, 0.5, 100)x2 = np.linspace(0.5, 1.5, 100)# Define the probability densitiesf1 = np.full_like(x1, 2)  # Probability density for first distributionf2 = np.full_like(x2, 1)  # Probability density for second distribution# Plot the first distributionplt.plot(x1, f1, label=\'U[0, 0.5]\', color=\'blue\')# Plot the second distributionplt.plot(x2, f2, label=\'U[0.5, 1.5]\', color=\'red\', linestyle=\'dashed\')# Add labels and legendplt.xlabel(\'x\')plt.ylabel(\'Probability Density\')plt.title(\'Uniform Distributions\')plt.legend()plt.grid(True)plt.show()

例: 设公共汽车每隔 5 分钟一班, 乘客到站是随机的, 则等车时间

服从 [0,5]上的均匀分布, 求

的密度函数并求某乘客随机地去乘车而候车时间不超过 3 分钟的概率?

解:

服从

上的均匀分布, 故其密度函数为:

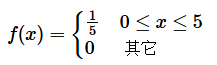
候车时间不超过 3 分钟的概率为:

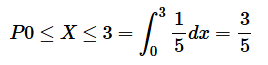
这份完整版的大模型 AI 学习资料已经上传CSDN，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】

指数（exponential）分布

指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔等。 许多电子产品的寿命分布一般服从指数分布。有的系统的寿命分布也可用指数分布来近似。它在可靠性研究中是最常用的一种分布形式。

设连续型随机变量

的概率密度为：

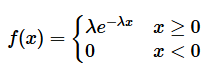
其中常数

, 则称

服从参数为

的指数分布, 可记成

 

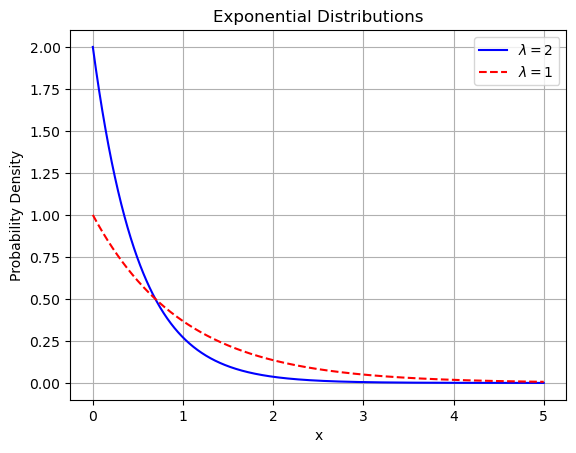
如下图所示。其中第一种分布使用实线表示

; 第二种分布使用虚线表示 

。​​​​​​​

import numpy as npimport matplotlib.pyplot as plt# Define the exponential distribution functionsdef exponential_pdf(x, lambda_):    return lambda_ * np.exp(-lambda_ * x)# Define the range for xx = np.linspace(0, 5, 1000)# Define the lambda valueslambda_1 = 2lambda_2 = 1# Calculate the probability densitiesy1 = exponential_pdf(x, lambda_1)y2 = exponential_pdf(x, lambda_2)# Plot the first distributionplt.plot(x, y1, label=r\'$\\lambda=2$\', color=\'blue\')# Plot the second distributionplt.plot(x, y2, label=r\'$\\lambda=1$\', color=\'red\', linestyle=\'dashed\')# Add labels and legendplt.xlabel(\'x\')plt.ylabel(\'Probability Density\')plt.title(\'Exponential Distributions\')plt.legend()plt.grid(True)plt.show()

例: 设某人造卫星的寿命

(单位: 年)服从参数为 2/3 的指数分布。若 3 颗这样的卫星同时升空投入使用, 求 2 年后 3 颗卫星都正常运行的概率?

解: 

的密度函数为:

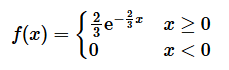
故 1 颗卫星 2 年后还正常运行的概率为:

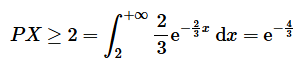
因此, 2 年后 3 颗卫星都正常的概率为:

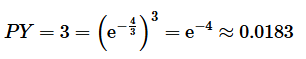
正态分布

正态分布又名高斯分布，是一个在数学、物理及工程等地方都非常重要的概率分布，在统计学的许多方面有着重大的影响力。若连续型随机变量

的密度函数为：

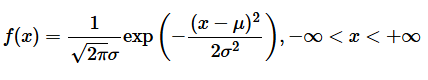
其中,

为均值、

为标准差, 

都为常数, 则称

服从参数为

的正态分布,简记为

。因其曲线呈钟形, 因此又经常称之为钟形曲线。通常所说的标准正态分布是

的正态分布。

正态分布的参数中, 

 决定了其位置, 标准差 

决定了分布的幅度。

具体来说, 若固定

而改变

的值, 则正态分布密度曲线沿着

轴平行移动, 而不改变其形状, 可见曲线的位置完全由参数

确定。

若固定 

 而改变 

 的值, 则当 

 越小时图形变得越陡峭; 反之,当 

 越大时图形变得越平缓,

如下图所示。其中第一种分布使用实线表示

;第二种分布使用虚线表示

。​​​​​​​

import numpy as npimport matplotlib.pyplot as plt# Define the normal distribution functiondef normal_pdf(x, mu, sigma):    return (1 / (sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu) / sigma)**2)# Define the range for xx = np.linspace(-3, 5, 1000)# Parameters for the normal distributionsmu1, sigma1 = 0, 0.5mu2, sigma2 = 1, 1# Calculate the probability densitiesy1 = normal_pdf(x, mu1, sigma1)y2 = normal_pdf(x, mu2, sigma2)# Plot the first distributionplt.plot(x, y1, label=r\'$\\mu=0, \\sigma=0.5$\', color=\'blue\')# Plot the second distributionplt.plot(x, y2, label=r\'$\\mu=1, \\sigma=1$\', color=\'red\', linestyle=\'dashed\')# Add labels and legendplt.xlabel(\'x\')plt.ylabel(\'Probability Density\')plt.title(\'Normal Distributions\')plt.legend()plt.grid(True)plt.show()

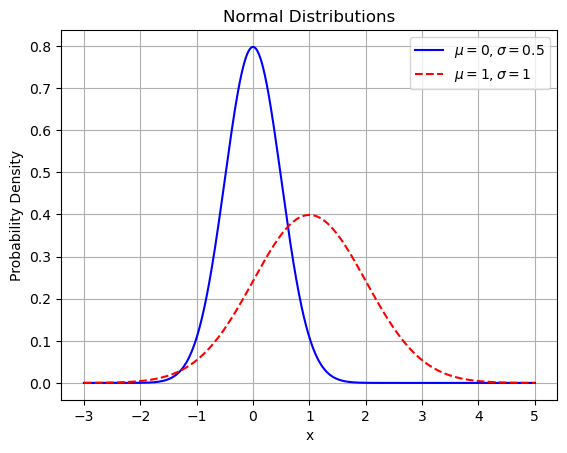
正态分布中一些值得注意的量：

• 密度函数关于平均值对称。

• 平均值与它的众数以及中位数同一数值。

• 68.268949%的面积在平均数左右的一个标准差范围内。

• 95.449974%的面积在平均数左右两个标准差的范围内。

• 99.730020%的面积在平均数左右三个标准差的范围内。

• 99.993666%的面积在平均数左右四个标准差的范围内。

在实际应用上，常考虑一组数据具有近似于正态分布的概率分布。

若其假设正确，则约68.3%数值分布在距离平均值有1个标准差之内的范围，约95.4%数值分布在距离平均值有2个标准差之内的范围，以及约99.7%数值分布在距离平均值有3个标准差之内的范围。

称为“68-95-99.7法则”或“经验法则”。

Z值与标准化

可以通过计算随机变量的Z值（z-score），得知其距离均值有多少个标准差。Z值的计算公式为：

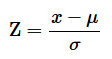
其中

是随机变量的值, 

是总体均值, 

是总体标准差。当

时, 正态分布就成为标准正态分布, 记作

 。

值将两组或多组数据转化为无单位的 
 

 score 分值, 使得数据标准统一化, 提高了数据可比性, 同时也削弱了数据解释性。 z 值的量代表着实测值和总体平均值之间的距离, 是以标准差为单位计算。大于均值的实测值会得到一个正数的 z 值,小于均值的实测值会得到一个负数的 z 值。

数据分析与挖掘中，很多方法需要样本符合一定的标准，如果需要分析的诸多自变量不是同一个量级，就会给分析工作造成困难，甚至影响后期建模的精准度。举个例子：

• 假设：A班级的平均分是80，标准差是10，A考了90分；B班的平均分是400，标准差是100，B考了600分。A和B谁的成绩好？

• 这可以计算得出，A的Z-score是（90-80）/10=1，B的Z-score（600-400）/100=2是。因此B的成绩更为优异。

通过Z-score可以有效的把数据转换为统一的标准，并进行比较。但是需要注意，Z-score本身没有实际意义，它的现实意义需要在比较中得以实现，这也是Z-score的缺点之一。

Z-score的另一个缺点是估算Z-score需要总体的平均值与方差，但是这一值在真实的分析与挖掘中很难得到，大多数情况下是用样本的均值与标准差替代。

正态分布为什么如此重要？

正态分布是最常见也是最重要的一种分布，自然界及社会生活、生产实际中很多随机变量都服从或近似服从正态分布，例如产品的各种质量指标、测量误差、某地区的年降雨量和成年人的身高等。

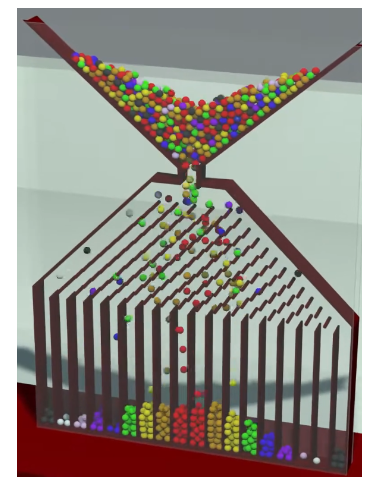
• 一个经典的例子是高尔顿顶板：

  • 高尔顿顶板由一个垂直放置的板子构成，板子上有许多水平排列的小钉子，钉子之间有一定间隔。板子的顶部有一个漏斗，用于让小球（通常是钢珠）通过。小球从漏斗口依次落下，碰到钉子后随机地向左或向右弹跳，继续向下掉落，直到到底部的多个格子中。

  • 当大量小球从漏斗中落下时，它们经过钉子的随机弹跳后，最终落在每个格子中的小球数量形成了一个钟形曲线，即正态分布。

• 高尔顿顶板的关键点：

  • 当小球数量足够大时，个体行为的随机性被群体行为的稳定性所覆盖，形成了有规律的分布。这被称为大数定律

  • 无论小球的初始分布如何，当其经过多次独立的随机过程后，最终的分布趋向于正态分布。这是正态分布在统计学和自然现象中如此普遍的重要原因。这被称为中心极限定理

大数定律与中心极限定理是统计学家总结出的自然现象，是概率统计的基石。很多定理和推论都是基于它们之上的研究。

 三、大模型风口已至：月薪30K+的AI岗正在批量诞生

2025年大模型应用呈现爆发式增长，根据工信部最新数据：

国内大模型相关岗位缺口达47万

初级工程师平均薪资28K

70%企业存在\"能用模型不会调优\"的痛点

真实案例：某二本机械专业学员，通过4个月系统学习，成功拿到某AI医疗公司大模型优化岗offer，薪资直接翻3倍！

 这份完整版的大模型 AI 学习资料已经上传CSDN，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】

四、如何学习大模型 AI ？

🔥AI取代的不是人类，而是不会用AI的人！麦肯锡最新报告显示：掌握AI工具的从业者生产效率提升47%，薪资溢价达34%！🚀

由于新岗位的生产效率，要优于被取代岗位的生产效率，所以实际上整个社会的生产效率是提升的。

但是具体到个人，只能说是：

“最先掌握AI的人，将会比较晚掌握AI的人有竞争优势”。

这句话，放在计算机、互联网、移动互联网的开局时期，都是一样的道理。

我在一线互联网企业工作十余年里，指导过不少同行后辈。帮助很多人得到了学习和成长。

我意识到有很多经验和知识值得分享给大家，也可以通过我们的能力和经验解答大家在人工智能学习中的很多困惑，所以在工作繁忙的情况下还是坚持各种整理和分享。但苦于知识传播途径有限，很多互联网行业朋友无法获得正确的资料得到学习提升，故此将并将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。

1️⃣ 提示词工程：把ChatGPT从玩具变成生产工具
2️⃣ RAG系统：让大模型精准输出行业知识
3️⃣ 智能体开发：用AutoGPT打造24小时数字员工

📦熬了三个大夜整理的《AI进化工具包》送你：
✔️ 大厂内部LLM落地手册（含58个真实案例）
✔️ 提示词设计模板库（覆盖12大应用场景）
✔️ 私藏学习路径图（0基础到项目实战仅需90天）

 

第一阶段（10天）：初阶应用

该阶段让大家对大模型 AI有一个最前沿的认识，对大模型 AI 的理解超过 95% 的人，可以在相关讨论时发表高级、不跟风、又接地气的见解，别人只会和 AI 聊天，而你能调教 AI，并能用代码将大模型和业务衔接。

*   大模型 AI 能干什么？
*   大模型是怎样获得「智能」的？
*   用好 AI 的核心心法
*   大模型应用业务架构
*   大模型应用技术架构
*   代码示例：向 GPT-3.5 灌入新知识
*   提示工程的意义和核心思想
*   Prompt 典型构成
*   指令调优方法论
*   思维链和思维树
*   Prompt 攻击和防范
*   …

第二阶段（30天）：高阶应用

该阶段我们正式进入大模型 AI 进阶实战学习，学会构造私有知识库，扩展 AI 的能力。快速开发一个完整的基于 agent 对话机器人。掌握功能最强的大模型开发框架，抓住最新的技术进展，适合 Python 和 JavaScript 程序员。

*   为什么要做 RAG
*   搭建一个简单的 ChatPDF
*   检索的基础概念
*   什么是向量表示（Embeddings）
*   向量数据库与向量检索
*   基于向量检索的 RAG
*   搭建 RAG 系统的扩展知识
*   混合检索与 RAG-Fusion 简介
*   向量模型本地部署
*   …

第三阶段（30天）：模型训练

恭喜你，如果学到这里，你基本可以找到一份大模型 AI相关的工作，自己也能训练 GPT 了！通过微调，训练自己的垂直大模型，能独立训练开源多模态大模型，掌握更多技术方案。

到此为止，大概2个月的时间。你已经成为了一名“AI小子”。那么你还想往下探索吗？

*   为什么要做 RAG
*   什么是模型
*   什么是模型训练
*   求解器 & 损失函数简介
*   小实验2：手写一个简单的神经网络并训练它
*   什么是训练/预训练/微调/轻量化微调
*   Transformer结构简介
*   轻量化微调
*   实验数据集的构建
*   …

第四阶段（20天）：商业闭环

对全球大模型从性能、吞吐量、成本等方面有一定的认知，可以在云端和本地等多种环境下部署大模型，找到适合自己的项目/创业方向，做一名被 AI 武装的产品经理。

*   硬件选型
*   带你了解全球大模型
*   使用国产大模型服务
*   搭建 OpenAI 代理
*   热身：基于阿里云 PAI 部署 Stable Diffusion
*   在本地计算机运行大模型
*   大模型的私有化部署
*   基于 vLLM 部署大模型
*   案例：如何优雅地在阿里云私有部署开源大模型
*   部署一套开源 LLM 项目
*   内容安全
*   互联网信息服务算法备案
*   …

学习是一个过程，只要学习就会有挑战。天道酬勤，你越努力，就会成为越优秀的自己。

如果你能在15天内完成所有的任务，那你堪称天才。然而，如果你能完成 60-70% 的内容，你就已经开始具备成为一名大模型 AI 的正确特征了。

这份完整版的大模型 AI 学习资料已经上传CSDN，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】