【DeepSeek系列】逐行讲解MLA朴素+吸收矩阵代码全新实现_mla的矩阵吸收

技术文档

引言

注意力机制作为大语言模型的核心组件，这么多年从最开始的 MHA 到现在最常用的 MQA、GQA，最主要的目的都是为了节省kv cache的大小。

MHA每一层需要存储【序列长度注意力头数每头维度】的大小，而MQA让每个头的k共享，需要存储的维度直接降低为【序列长度1每头维度】，但后面发现这样降的太多就导致性能下降，所以设计出了一种折中方案。GQA自定义多少个头共享一个k，最终维度变为【序列长度组数每头维度】

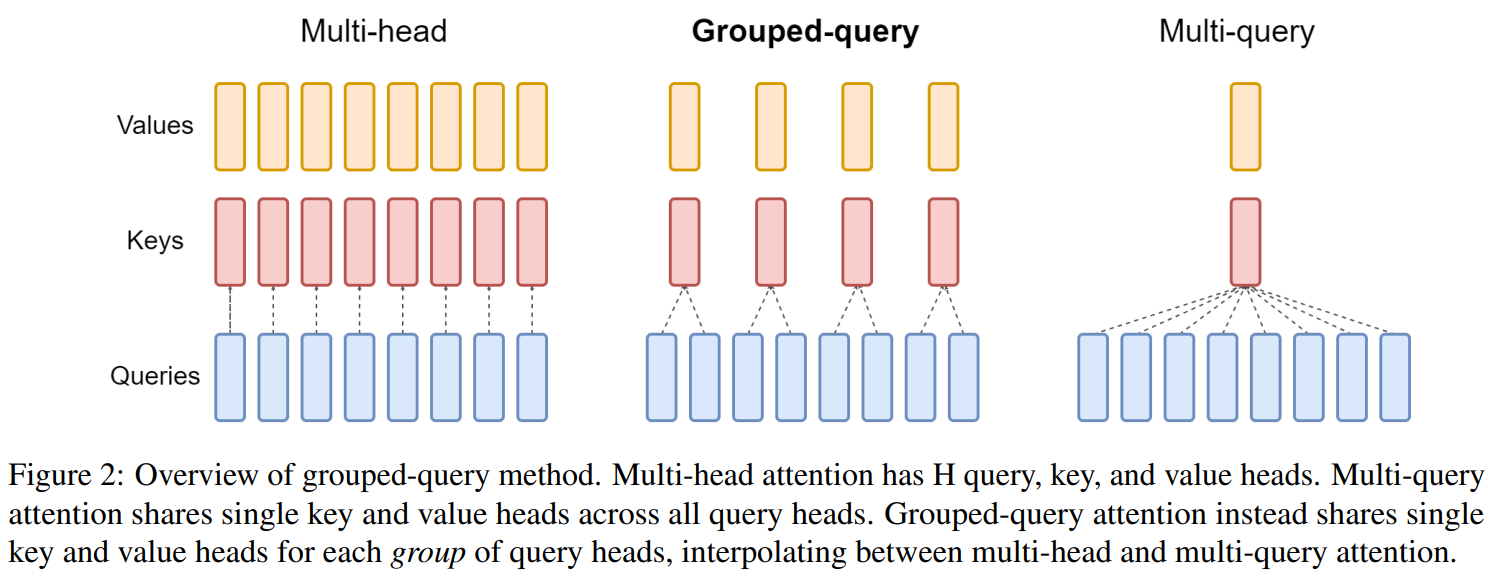
【DeepSeek系列】逐行讲解MLA朴素+吸收矩阵代码全新实现_mla的矩阵吸收

以下给出了GQA的计算结构图，这里设置的组数为4，MHA和MQA就是将这个组数修改为注意力头数或1。

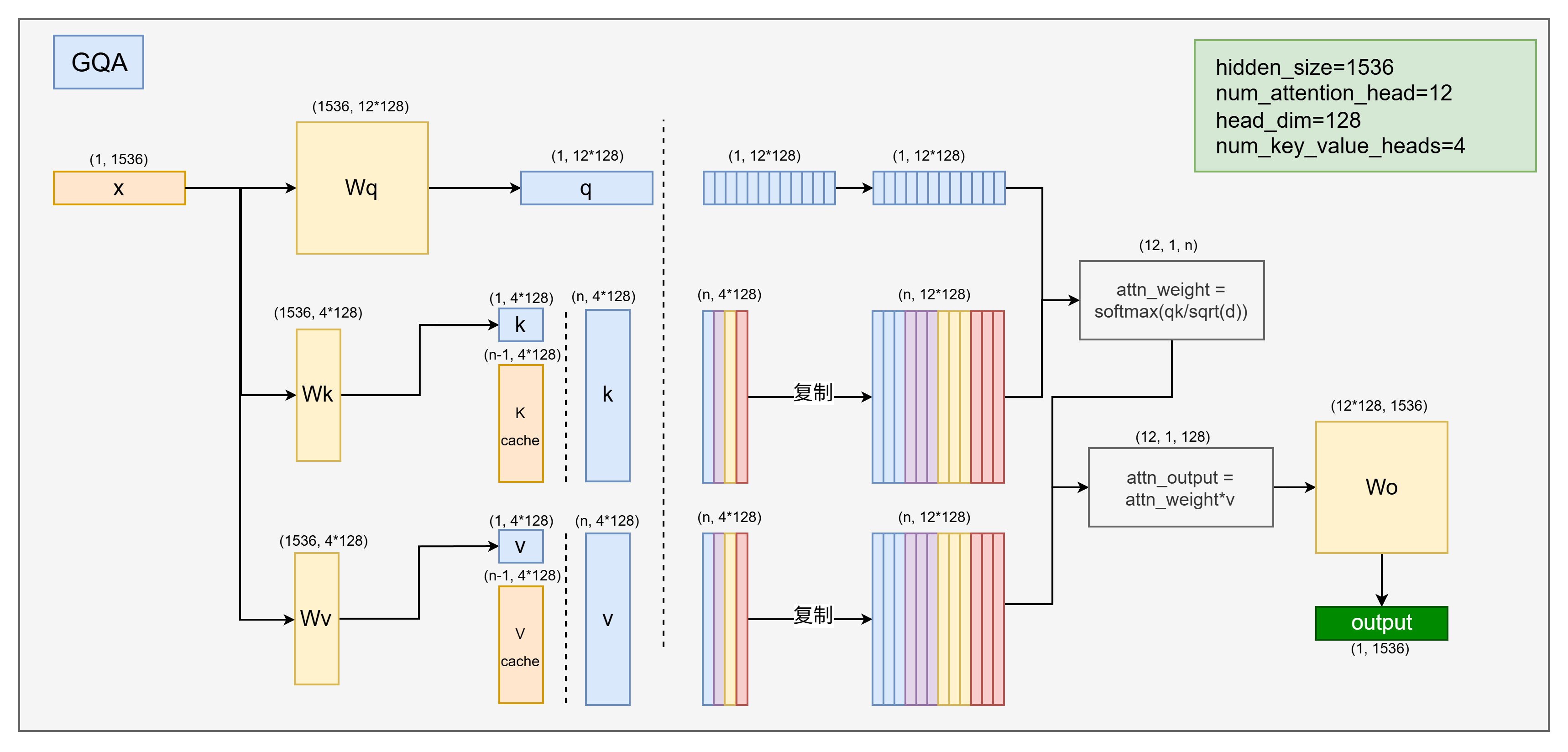
【DeepSeek系列】逐行讲解MLA朴素+吸收矩阵代码全新实现_mla的矩阵吸收

MLA 借鉴了LoRA的思路，使用一个降维矩阵将隐层维度降低，然后存储为kv cache，在注意力计算时，使用一个升维矩阵将kv cache升维，从而达到节省kv cache的目的，而且由于升降维矩阵的存在，性能并不会降低（实验证明反而会提高）。

到这个时候，网上已经有很多关于MLA理论的讲解了，但 MLA 听着简单，就是注意力降维、解耦旋转矩阵、吸收矩阵，但你真得搞懂它的内部细节了吗。
MLA 内部涉及10多个矩阵，绕来绕去都晕了，每一步具体怎么切分的，怎么转化维度的，如果让你清晰的描述出来，可能也会很难吧。

本文结合网络图和代码，一步一步详细讲解MLA都做了什么，那么多矩阵都是做什么用的，还请耐心观看。

针对每一个token的注意力计算，都是一个重复的过程，那我们就取中间的一步进行模拟MLA计算。注意这里的维度大小我直接按照deepseek的参数写具体值，这样更为清晰。本文中的矩阵及向量命名都遵守deepseek的命名。

MLA 数据流向

MLA朴素版

首先介绍MLA的常规计算
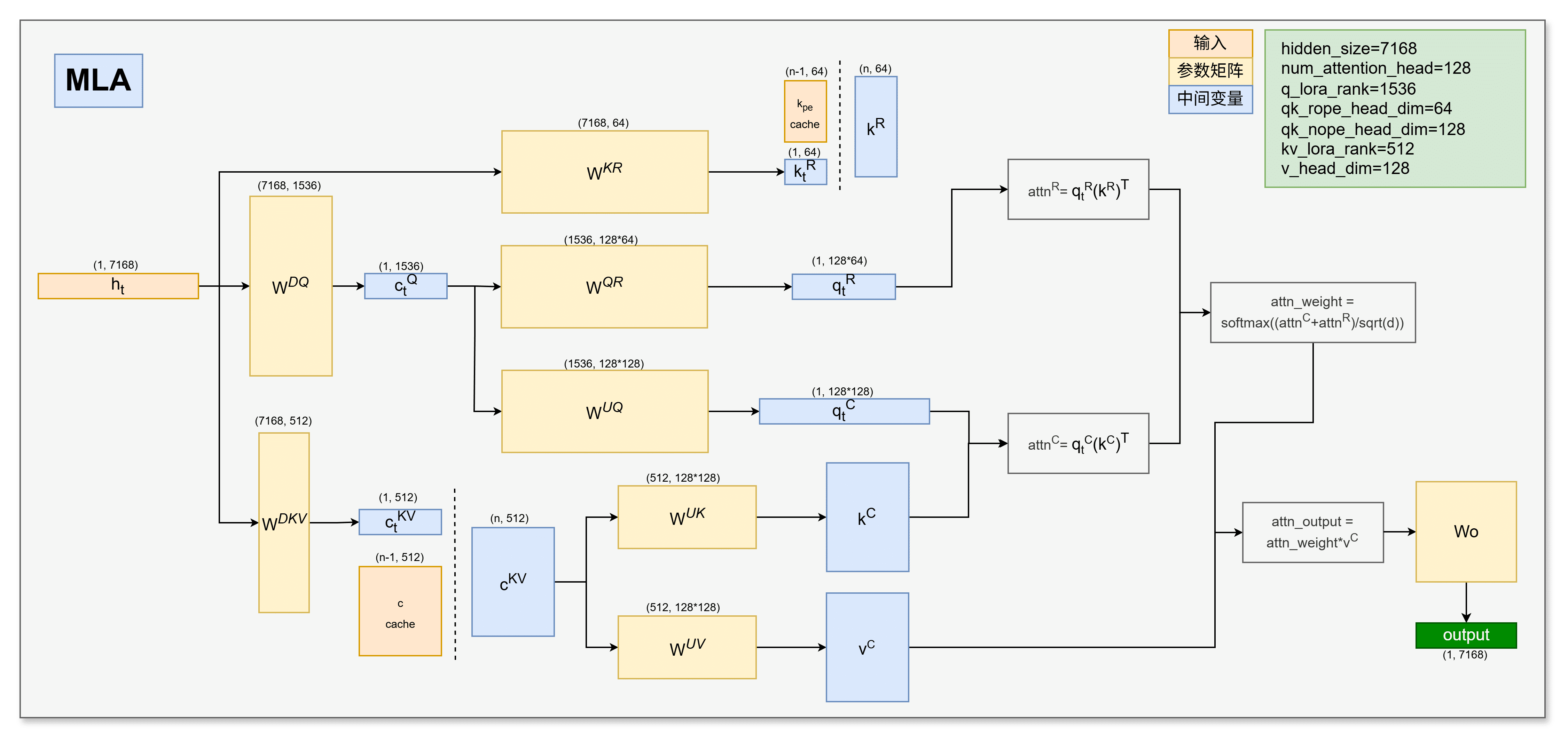
【DeepSeek系列】逐行讲解MLA朴素+吸收矩阵代码全新实现_mla的矩阵吸收

输入：首先注意力计算 forward 函数会输入隐层向量 hidden_state，记作 $h_t$ ，它的维度是[1, 7168]，因为推理时是一个token一个token进行处理的。

还会输入 kv cache，记作 $c^{KV}$ ，它的维度是[n-1, 512]，n-1是历史序列长度。

由于旋转位置编码解耦，所以还要输入一个 $k^R$ ，它的维度是[n, 64]，这里k的旋转位置编码在各个头是共享的，所以不需要128*64个。
计算q：首先基于 $h_t$ 计算当前 token 的 $q_t^C$ 和 $q_t^R$ ，即拆分成没有rope和带rope的。先将 $h_t$ 进行降维，得到 $c_t^Q=h_tW^{DQ}$ ，它的维度是 [1, 1536]。

然后与 $W^{UQ}$ 相乘，得到 $q_t^C=c_t^QW^{UQ}$ ，它的维度是 [1, 128*128]，代表128个头，每个头128个维度。

同理， $q_t^R=c_t^QW^{QR}$ 的维度是 [1, 128*64]。
计算c：然后将当前 token 转化成 c 作为 kv cache。

直接将 $h_t$ 降维，得到 $c_t^{KV}=h_tW^{DKV}$ ，它的维度是 [1, 512]。将其与历史 kv cache 拼接，记作 $c^{KV}$ ，它的维度是 [n, 512]。同时将本次的 $c^{KV}$ 存储下来，用于下次计算。
计算kv：处理 kv cache 即 $c^{KV}$ ，得到可计算的 k 和 v。

$k^C=c^{KV}W^{UK}$ ，它的维度是 [n, 128*128]。

$v^C=c^{KV}W^{UV}$ ，它的维度是 [n, 128*128]。

$k_t^R=h_tW^{KR}$ ，它的维度是 [1, 64]，与输入的 $k_{pe} cache$ 拼接到一起，得到 $k_t^R$ ，维度是 [n, 64]，注意这里每个头之间是共享的，所以不需要128*64个。但是在后续注意力计算的时候需要维度广播，复制出128份。
计算注意力权重：

$attn^C = q_t^C(k^C)^T$ ，它的维度是 [n, 128]。

$attn^R = q_t^R(k^R)^T$ ，它的维度是 [n, 128]。

$attn = attn^C + attn^R$

$attn\\_weight = softmax(\\frac{attn}{\\sqrt{d}})$

这里带rope和不带rope的注意力是分开算的，根据矩阵的性质，分开计算再相加与合并后计算的结果是相同的。

其等价于：

$attn = [q_t^C; q_t^R]([k^C; k^R])^T$
与v相乘： $attn\\_output = attn\\_weight * v^C$
最终输出： $output = attn\\_output * W^{O}$

总体公式为（当前token转化成c需要单独计算，且忽略rope的部分）：

$softmax(\\frac{(h_tW^{DQ}W^{UQ})(c^{KV}W^{UK})^T}{\\sqrt{d}}) (c^{KV}W^{UV}) W^{O} \\\\ = softmax(\\frac{h_tW^{DQ}W^{UQ}W^{UK^T}c^{KV^T}}{\\sqrt{d}})c^{KV}W^{UV}W^{O}$

MLA 吸收矩阵版

接下来介绍MLA吸收矩阵的计算方式
MLA 吸收矩阵数据流向图
上面总体公式中 $W^{UQ}W^{UK^T}$ 是挨着的， $W^{UV}W^{O}$ 也是挨着的，所以可以提前合并成一个矩阵，记作 $W^{UQK}$ 和 $W^{UVO}$ ，这样每次推理就不用进行两次矩阵运算了，加快推理速度，这个就叫做吸收矩阵 (absorb matrix)。

那吸收之后的总体公式变为：

$softmax(\\frac{h_tW^{DQ}W^{UQK}c^{KV^T}}{\\sqrt{d}})c^{KV}W^{UVO}$

那整体计算流程就变成了：

输入：与常规相同
计算q：还是首先基于 $h_t$ 计算当前 token 的 $q_t^C$ 和 $q_t^R$ 。首先还是将 $h_t$ 降维，得到 $c_t^Q=h_tW^{DQ}$ ，它的维度是 [1, 1536]。

$q_t^R$ 与常规相同： $q_t^R=c_t^QW^{QR}$ 的维度是 [1, 128*64]。

$q_t^C$ 直接一步到位乘以吸收矩阵： $q_t^C=c_t^QW^{UQK}=h_tW^{DQ}W^{UQK}$ ，它的维度是 [1, 128*512]。
计算c：与常规相同
计算kv：这步删除掉处理 $k^C$ 和 $v^C$ 的步骤，不需要提前分解 $c^{KV}$ 了，但 $k^R$ 与常规相同。
计算注意力权重：

$attn^C = q_t^C(c^{KV})^T$ ，它的维度是 [n, 128]。

$attn^R = q_t^R(k^R)^T$ ，与常规一样，它的维度是 [n, 128]。

$attn = attn^C + attn^R$

$attn\\_weight = softmax(\\frac{attn}{\\sqrt{d}})$
与v相乘+最终输出：两步合为一步， $output = attn\\_weight * c^{KV}W^{UVO}$

至此，MLA就介绍完了，现在你还能复述一遍 MLA 的计算流程吗？那些矩阵还能分得清吗？如果都能搞懂，说明你真得掌握了 MLA，可以去看看 flash MLA 了[狗头]。

代码详解

这里给出MLA实现的代码，参考transformers其他模型注意力部分的实现原理，传入kv cache的同时要传出kv cache。以下代码完全按照上述MLA数据流向图设计的，与图对比基本都能看懂。

首先引入ROPE+RMSNorm 代码初始化

# 改编自：https://github.com/flashinfer-ai/flashinfer/blob/738460ff82e2230ebcc8dff50e49e1d6278e011a/tests/test_mla_decode_kernel.pyfrom typing import Optional, Tupleimport timeimport torchfrom torch import nndef precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0, use_scaled: bool = False): freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim)) t = torch.arange(end, device=freqs.device, dtype=torch.float32) freqs = torch.outer(t, freqs) freqs_cis = torch.polar(torch.ones_like(freqs), freqs) # complex64 return freqs_cisdef reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor): ndim = x.ndim assert 0 <= 1 < ndim assert freqs_cis.shape == (x.shape[1], x.shape[-1]) shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)] return freqs_cis.view(*shape)def apply_rotary_emb( xq: torch.Tensor, xk: torch.Tensor, freqs_cis: torch.Tensor,) -> Tuple[torch.Tensor, torch.Tensor]: xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2)) xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2)) freqs_cis = reshape_for_broadcast(freqs_cis, xq_) xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3) xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3) return xq_out.type_as(xq), xk_out.type_as(xk)class DeepseekV2RMSNorm(nn.Module): def __init__(self, hidden_size, eps=1e-6): \"\"\" DeepseekV2RMSNorm is equivalent to T5LayerNorm \"\"\" super().__init__() self.weight = nn.Parameter(torch.ones(hidden_size)) self.variance_epsilon = eps def forward(self, hidden_states): input_dtype = hidden_states.dtype hidden_states = hidden_states.to(torch.float32) variance = hidden_states.pow(2).mean(-1, keepdim=True) hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon) return (self.weight * hidden_states).to(input_dtype)

朴素版的MLA代码代码

class DeepseekV2AttentionVanilla(nn.Module): def __init__(self): super().__init__() # 以 deepseekv2 参数为准 self.hidden_size = 7168 self.num_heads = 128 self.q_lora_rank = 1536 self.qk_rope_head_dim = 64 self.kv_lora_rank = 512 self.v_head_dim = 128 self.qk_nope_head_dim = 128 self.q_head_dim = 192 # 192 = 128 + 64 = config.qk_nope_head_dim + config.qk_rope_head_dim self.rope_theta = 10000 self.q_a_layernorm = DeepseekV2RMSNorm(self.q_lora_rank) self.softmax_scale = self.q_head_dim ** (-0.5) # W^DQ ~ [7168, 1536] self.W_DQ = nn.Linear(self.hidden_size, self.q_lora_rank, bias=False) # W^UQ ~ [1536, 128*128] self.W_UQ = nn.Linear(self.q_lora_rank, self.num_heads * self.qk_nope_head_dim, bias=False) # W^QR ~ [1536, 128*64] self.W_QR = nn.Linear(self.q_lora_rank, self.num_heads * self.qk_rope_head_dim, bias=False) # W^KR ~ [1536, 64] self.W_KR = nn.Linear(self.hidden_size, self.qk_rope_head_dim, bias=False) # W^DKV ~ [7168, 512] self.W_DKV = nn.Linear(self.hidden_size, self.kv_lora_rank, bias=False) # W^UK ~ [512, 128*128] self.W_UK = nn.Linear(self.kv_lora_rank, self.num_heads * self.qk_nope_head_dim, bias=False) # W^UV ~ [512, 128*128] self.W_UV = nn.Linear(self.kv_lora_rank, self.num_heads * self.v_head_dim, bias=False) # W^O ~ [128*128, 7168] self.W_O = nn.Linear(self.num_heads * self.v_head_dim, self.hidden_size, bias=False) def run_decode( self, hidden_states: torch.Tensor, compressed_kv_normed_cache: torch.Tensor, k_pe_cache: torch.Tensor, ) -> Tuple[torch.Tensor, Optional[torch.Tensor], Optional[Tuple[torch.Tensor]]]: # 获取维度：[batch_size, query_length=1, hidden_size] bsz, q_len, _ = hidden_states.size() # 当前step输入的x，经过W_DQ，得到 [batch_size, 1, q_lora_rank] c_t_Q = self.q_a_layernorm(self.W_DQ(hidden_states)) # 再经过W_UQ，得到 [batch_size, 1, num_heads=128 * qk_nope_head_dim=128] q_t_C = self.W_UQ(c_t_Q) # 再经过W_QR，得到 [batch_size, 1, num_heads=128 * qk_rope_head_dim=64] q_t_R = self.W_QR(c_t_Q).view(bsz, -1, self.num_heads, self.qk_rope_head_dim) # 再经过W_KR，得到 [batch_size, 1, qk_rope_head_dim=64] # 将当前step的k_t_R添加到k_pe_cache的最后一个位置，得到新的k_pe_cache k_t_R = self.W_KR(hidden_states) k_pe_cache = torch.cat([k_pe_cache, k_t_R], dim=1) # 将最后一个维度拆开，方便注意力计算 q_t_C = q_t_C.view(bsz, q_len, self.num_heads, self.qk_nope_head_dim).transpose(1, 2) c_t_KV = self.W_DKV(hidden_states) compressed_kv_normed_cache = torch.cat([compressed_kv_normed_cache, c_t_KV], dim=1) k_C = self.W_UK(compressed_kv_normed_cache).view(bsz, -1, self.num_heads, self.qk_nope_head_dim).transpose(1, 2) v_C = self.W_UV(compressed_kv_normed_cache).view(bsz, -1, self.num_heads, self.v_head_dim).transpose(1, 2) # 计算位置编码，暂时不用管，与其他的RoPE计算方式类似，最终得到旋转之后的 q_pe, k_pe freqs_cis = precompute_freqs_cis(self.qk_rope_head_dim, compressed_kv_normed_cache.shape[1], self.rope_theta, use_scaled=False).to(q_t_R.device) q_t_R, k_R = apply_rotary_emb( q_t_R.repeat(1, compressed_kv_normed_cache.shape[1], 1, 1), k_pe_cache.unsqueeze(2), freqs_cis, ) q_t_R = q_t_R[:, -1:, :, :].transpose(1, 2) k_R = k_R.transpose(1, 2).repeat(1, self.num_heads, 1, 1) attn_R = torch.matmul(q_t_R, k_R.transpose(2, 3)) attn_C = torch.matmul(q_t_C, k_C.transpose(2, 3)) attn_weights = (attn_R + attn_C) * self.softmax_scale attn_weights = nn.functional.softmax(attn_weights, dim=-1, dtype=torch.float32).to(q_t_C.dtype) # 将注意力权重和v相乘，得到注意力输出，维度为[batch_size, num_heads, q_len, v_head_dim=128] attn_output = torch.matmul(attn_weights, v_C) # 将最后一个维度展开，得到[batch_size, num_heads, q_len, v_head_dim=128] attn_output = attn_output.transpose(1, 2).reshape( bsz, q_len, self.num_heads * self.v_head_dim ) # 将注意力输出和W^O相乘，得到最终的输出，维度为[batch_size, q_len, hidden_size=7168] output = self.W_O(attn_output) return output, attn_weights, compressed_kv_normed_cache, k_pe_cachemla_vanilla = DeepseekV2AttentionVanilla()batch_size = 6kv_len = 10hidden_states = torch.randn([batch_size, 1, mla_vanilla.hidden_size])compressed_kv_normed_cache = torch.randn([batch_size, kv_len, mla_vanilla.kv_lora_rank])k_pe_cache = torch.randn([batch_size, kv_len, mla_vanilla.qk_rope_head_dim])start_time = time.time()for i in range(10): output_vanilla, attn_weights, compressed_kv_normed_cache, k_pe_cache = mla_vanilla.run_decode( hidden_states, compressed_kv_normed_cache, k_pe_cache ) # print(\'output_vanilla.shape\', output_vanilla.shape) # print(\'attn_weights.shape\', attn_weights.shape) # print(\'compressed_kv_normed_cache.shape\', compressed_kv_normed_cache.shape) # print(\'k_pe_cache.shape\', k_pe_cache.shape) # print(\'-\'*70)end_time = time.time()print(\'time\', end_time - start_time)

MLA 吸收矩阵版的代码

from torch import nnclass DeepseekV2AttentionMatAbsorbDecode(nn.Module): def __init__(self): super().__init__() self.hidden_size = 7168 self.num_heads = 128 self.q_lora_rank = 1536 self.qk_rope_head_dim = 64 self.kv_lora_rank = 512 self.v_head_dim = 128 self.qk_nope_head_dim = 128 self.q_head_dim = 192 # 192 = 128 + 64 = config.qk_nope_head_dim + config.qk_rope_head_dim self.rope_theta = 10000 self.q_a_layernorm = DeepseekV2RMSNorm(self.q_lora_rank) self.softmax_scale = self.q_head_dim ** (-0.5) # W^DQ ~ [7168, 1536] self.W_DQ = nn.Linear(self.hidden_size, self.q_lora_rank, bias=False) # W^UQ ~ [1536, 128*128] self.W_UQ = nn.Linear(self.q_lora_rank, self.num_heads * self.qk_nope_head_dim, bias=False) # W^QR ~ [1536, 128*64] self.W_QR = nn.Linear(self.q_lora_rank, self.num_heads * self.qk_rope_head_dim, bias=False) # W^KR ~ [1536, 64] self.W_KR = nn.Linear(self.hidden_size, self.qk_rope_head_dim, bias=False) # W^DKV ~ [7168, 512] self.W_DKV = nn.Linear(self.hidden_size, self.kv_lora_rank, bias=False) # W^UK ~ [512, 128*128] self.W_UK = nn.Linear(self.kv_lora_rank, self.num_heads * self.qk_nope_head_dim, bias=False) # W^UV ~ [512, 128*128] self.W_UV = nn.Linear(self.kv_lora_rank, self.num_heads * self.v_head_dim, bias=False) # W^O ~ [128*128, 7168] self.W_O = nn.Linear(self.num_heads * self.v_head_dim, self.hidden_size, bias=False) # 由于nn.Linear初始化的时一个对象，权重矩阵只是对象中的一个类，没法直接两个矩阵相乘 # 所以需要用.weight来取出来，而且因为.weight的维度与初始化是反的，所以需要用t()来转置 # W_UQ_absorb ~ [1536, 128, 128] W_UQ_absorb = self.W_UQ.weight.t().view(self.q_lora_rank, self.num_heads, self.qk_nope_head_dim) # W_UK_absorb ~ [512, 128, 128] W_UK_absorb = self.W_UK.weight.t().view(self.kv_lora_rank, self.num_heads, self.qk_nope_head_dim) # W_UV_absorb ~ [512, 128, 128] W_UV_absorb = self.W_UV.weight.t().view(self.kv_lora_rank, self.num_heads, self.v_head_dim) # W_O_absorb ~ [7168, 128, 128] W_O_absorb = self.W_O.weight.view(self.hidden_size, self.num_heads, self.v_head_dim) # 吸收矩阵：将W_UQ和W_UK合并，得到新的W_UQK，维度为[1536, 128, 128] # q~q_lora_rank n~num_heads d~qk_nope_head_dim l~kv_lora_rank # 这里把n当做batch_size，也就是矩阵相乘不会影响的那个维度，矩阵qd与dl相乘，得到ql，加上刚才的n，所以得到qnl # 再将其flatten展平，得到[1536, 65536] self.W_UQK = torch.einsum(\"q n d, l n d -> q n l\", W_UQ_absorb, W_UK_absorb).flatten(start_dim=1) # 吸收矩阵，将W_UV和W_O合并，得到新的W_UV_O，维度为[128, 512, 7168] # l~kv_lora_rank n~num_heads d~v_head_dim h~hidden_size # 这里把n当做batch_size，也就是矩阵相乘不会影响的那个维度，矩阵ld与dh相乘，得到lh，加上刚才的n，并把n放到最前面，所以得到nlh # 再将其flatten展平，得到[65536, 7168] self.W_UV_O = torch.einsum(\"l n d, h n d -> n l h\", W_UV_absorb, W_O_absorb).flatten(start_dim=0, end_dim=1) def run_decode( self, hidden_states: torch.Tensor, compressed_kv_normed_cache: torch.Tensor, k_pe_cache: torch.Tensor, ) -> Tuple[torch.Tensor, Optional[torch.Tensor], Optional[Tuple[torch.Tensor]]]: # 获取维度：[batch_size, query_length=1, hidden_size] bsz, q_len, _ = hidden_states.size() # 当前step输入的x，经过W_DQ，得到 [batch_size, 1, q_lora_rank] c_t_Q = self.q_a_layernorm(self.W_DQ(hidden_states)) # 再经过W_UQ，得到 [batch_size, 1, num_heads=128 * qk_nope_head_dim=128] q_t_C = torch.matmul(c_t_Q, self.W_UQK) # 再经过W_QR，得到 [batch_size, 1, num_heads=128 * qk_rope_head_dim=64] q_t_R = self.W_QR(c_t_Q).view(bsz, -1, self.num_heads, self.qk_rope_head_dim) # 再经过W_KR，得到 [batch_size, 1, qk_rope_head_dim=64] # 将当前step的k_t_R添加到k_pe_cache的最后一个位置，得到新的k_pe_cache k_t_R = self.W_KR(hidden_states) k_pe_cache = torch.cat([k_pe_cache, k_t_R], dim=1) # 将最后一个维度拆开，方便注意力计算 q_t_C = q_t_C.view(bsz, q_len, self.num_heads, self.kv_lora_rank).transpose(1, 2) c_t_KV = self.W_DKV(hidden_states) compressed_kv_normed_cache = torch.cat([compressed_kv_normed_cache, c_t_KV], dim=1) # 计算位置编码，暂时不用管，与其他的RoPE计算方式类似，最终得到旋转之后的 q_pe, k_pe freqs_cis = precompute_freqs_cis(self.qk_rope_head_dim, compressed_kv_normed_cache.shape[1], self.rope_theta, use_scaled=False).to(q_t_R.device) q_t_R, k_R = apply_rotary_emb( q_t_R.repeat(1, compressed_kv_normed_cache.shape[1], 1, 1), k_pe_cache.unsqueeze(2), freqs_cis, ) q_t_R = q_t_R[:, -1:, :, :].transpose(1, 2) k_R = k_R.transpose(1, 2).repeat(1, self.num_heads, 1, 1) attn_R = torch.matmul(q_t_R, k_R.transpose(2, 3)) attn_C = torch.matmul(q_t_C, compressed_kv_normed_cache.unsqueeze(1).transpose(2, 3)) attn_weights = (attn_R + attn_C) * self.softmax_scale attn_weights = nn.functional.softmax(attn_weights, dim=-1, dtype=torch.float32).to(q_t_C.dtype) # attn_weights * c^KV * W^UVO attn_output = torch.matmul( attn_weights.squeeze(2), # [bsz, 128, kv_len] compressed_kv_normed_cache, # [bsz, kv_len, 512] ).reshape(bsz, self.num_heads * self.kv_lora_rank) output = torch.matmul(attn_output, self.W_UV_O,) # W_UV_O ~ [65536, 7168] return output, attn_weights, compressed_kv_normed_cache, k_pe_cache bsz = 6kv_len = 10hidden_states = torch.randn([bsz, 1, 7168])compressed_kv_normed_cache = torch.randn([bsz, kv_len, 512])k_pe_cache = torch.randn([bsz, kv_len, 64])mla_mat_absorb = DeepseekV2AttentionMatAbsorbDecode()start_time = time.time()for i in range(10): output_vanilla, attn_weights, compressed_kv_normed_cache, k_pe_cache = mla_mat_absorb.run_decode( hidden_states, compressed_kv_normed_cache, k_pe_cache ) # print(\'output_vanilla.shape\', output_vanilla.shape) # print(\'attn_weights.shape\', attn_weights.shape) # print(\'compressed_kv_normed_cache.shape\', compressed_kv_normed_cache.shape) # print(\'k_pe_cache.shape\', k_pe_cache.shape) # print(\'-\'*70)end_time = time.time()print(\'time\', end_time - start_time)

计算量对比

其实两个矩阵吸收之后的维度是比两个矩阵相加的参数量是多的，但是在计算时由于n的存在，n越大，吸收矩阵的计算量越小，所以加速越多。

实验表明，n=26吸收后计算量更低，但实际使用prompt的长度都不止26，所以吸收之后肯定会变快。

# 实际吸收后的矩阵更大了，计算量更多了，但由于n的存在，序列越长，总体计算量越小n=20000W_UQK = 1536*128*128 + 512*128*128*n + 128*128*nW_UQK_absorbed = 1536*128*512 + 128*512*nW_UV_O = 512*128*128*n + 128*128*n + 128*128*7168W_UV_O_absorbed = 128*512*7168 + 128*512*nprint(\'W_UQK吸收前：\', W_UQK)print(\'W_UQK吸收后：\', W_UQK_absorbed)print(\'W_UV_O吸收前：\', W_UV_O)print(\'W_UV_O吸收后：\', W_UV_O_absorbed)print(\'全部吸收前：\', W_UQK + W_UV_O)print(\'全部吸收后：\', W_UQK_absorbed + W_UV_O_absorbed)# W_UQK吸收前： 168125005824# W_UQK吸收后： 1411383296# W_UV_O吸收前： 168217280512# W_UV_O吸收后： 1780482048# 全部吸收前： 336342286336# 全部吸收后： 3191865344

参考资料

https://arxiv.org/pdf/2405.04434
https://kexue.fm/archives/10091
https://mp.weixin.qq.com/s/E7NwwMYw14FRT6OKzuVXFA
https://huggingface.co/deepseek-ai/DeepSeek-V2/blob/main/modeling_deepseek.py#L682
https://github.com/flashinfer-ai/flashinfer/blob/738460ff82e2230ebcc8dff50e49e1d6278e011a/tests/test_mla_decode_kernel.py

【DeepSeek系列】逐行讲解MLA朴素+吸收矩阵代码全新实现_mla的矩阵吸收

引言

MLA 数据流向

MLA朴素版

MLA 吸收矩阵版

代码详解

参考资料

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

【DeepSeek系列】逐行讲解MLA朴素+吸收矩阵代码全新实现_mla的矩阵吸收

引言

MLA 数据流向

MLA朴素版

MLA 吸收矩阵版

代码详解

参考资料

相关问题

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载