LLM：Day3

上午：理论学习（神经网络基础 + RNN 系列）

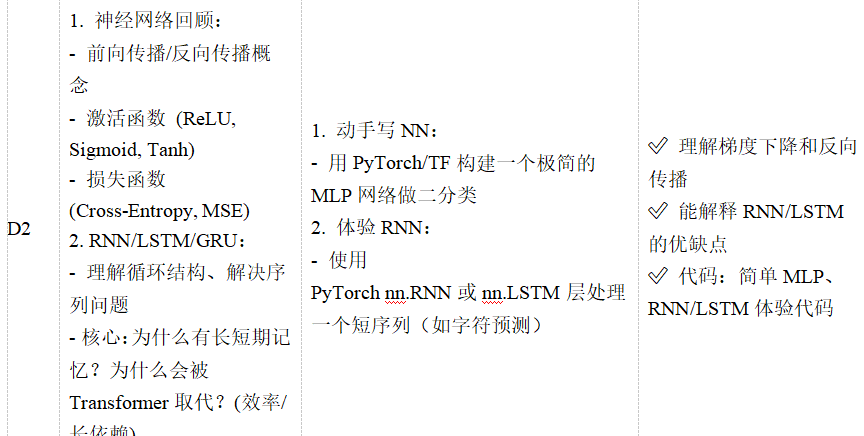
1. 神经网络回顾（搞懂 “计算机如何学习” 的基本逻辑）

（1）核心概念：前向传播与反向传播（用 “学生做题” 类比）

• 前向传播：

  • 类比：学生做新题时，用已学知识一步步推导答案（从输入到输出的计算过程）。
  • 专业解释：输入数据（如文本、图片）通过神经网络的层（如线性层、激活函数），最终得到预测结果（如 “正面情绪”“负面情绪”）。
  • 例：用一个简单神经网络判断 “1+1=？”，输入 “1,1”，通过计算得到预测结果 “2.1”（接近正确答案）。

• 反向传播：

  • 类比：学生做完题后，老师批改指出错误（比如 “答案应该是 2，你算成 2.1 了”），学生根据错误调整解题思路。
  • 专业解释：通过 “损失函数” 计算预测结果与正确答案的差距（如 “2.1-2=0.1”），然后从输出层反向调整网络中 “权重”（类似解题步骤中的系数），减少差距。
  • 核心：神经网络通过反向传播 “自学”，不断优化预测能力（这是 AI 能 “学习” 的关键）。

（2）激活函数（给神经网络 “非线性能力”，否则就是简单计算器）

函数名称 通俗作用（小白版） 例子（什么时候用） ReLU 让网络 “忽略不重要的信号”（输入为负时输出 0，正数不变） 几乎所有神经网络的隐藏层（如 BERT、CNN 的中间层） Sigmoid 把输出压缩到 0-1 之间（可表示 “概率”） 二分类问题的输出层（如 “是垃圾邮件（1）还是正常邮件（0）”） Tanh 把输出压缩到 - 1 到 1 之间（比 Sigmoid 更对称） RNN 的隐藏层（处理序列数据时更稳定）

• 为什么需要：如果没有激活函数，神经网络就是 “线性函数”（类似 y=ax+b），无法处理复杂问题（如文本分类、图像识别）。激活函数让网络能学习非线性关系（比如 “‘喜欢’和‘讨厌’的区别不仅是词本身，还和上下文有关”）。

（3）损失函数（衡量 “预测有多差”，类似 “错题本”）

• 作用：计算预测结果与正确答案的差距（差距越大，损失值越高），反向传播就是根据这个差距调整网络。
• 常见损失函数：
  • Cross-Entropy（交叉熵）：用于分类问题（如文本分类、情感分析），衡量 “预测的类别概率” 与 “实际类别” 的差距。
    • 例：正确答案是 “正面”，模型预测 “正面概率 90%”→损失小；预测 “正面概率 10%”→损失大。
  • MSE（均方误差）：用于回归问题（如预测房价、温度），计算预测值与实际值的平方差。
    • 例：实际房价 100 万，模型预测 90 万→MSE=(100-90)²=100；预测 99 万→MSE=1（损失更小）。

2. RNN/LSTM/GRU（处理 “序列数据” 的神经网络，文本是典型的序列）

（1）为什么需要循环神经网络？

• 文本、语音、视频都是 “序列数据”（有先后顺序，比如 “我喜欢你” 和 “你喜欢我” 意思不同）。
• 普通神经网络（如 MLP）处理数据时 “忘记过去”（每个输入独立处理），无法理解序列的顺序关系。
• RNN 的核心：有一个 “记忆单元”，处理当前输入时会结合 “上一步的记忆”（类似人类说话时会参考前半句）。

（2）RNN 的结构与问题（为什么会被 Transformer 取代？）

• 结构：简单说就是 “输入→结合上一步的隐藏状态→输出 + 更新隐藏状态”，循环处理序列中的每个元素（如每个词）。
• 缺点：
  • 长距离依赖问题：处理长文本时（如 100 个词的句子），早期的信息（如第 1 个词）会被 “遗忘”，无法影响后期预测（比如 “小明…… 他”，RNN 可能忘记 “他” 指的是 “小明”）。
  • 效率低：必须按顺序处理（第 2 个词的计算依赖第 1 个，无法并行），训练慢。

（3）LSTM/GRU：解决 RNN 的 “健忘症”

• LSTM（长短期记忆网络）：

  • 改进：增加 “门控机制”（输入门、遗忘门、输出门），类似 “选择性记忆”（重要信息记下来，无关信息忘记）。
  • 例：处理 “小明…… 昨天…… 他” 时，LSTM 能记住 “小明” 是 “他” 的指代对象。

• GRU（门控循环单元）：

  • 改进：简化 LSTM 的结构（合并门控），在保持效果的同时更快。

• 为什么仍被 Transformer 取代：

  • 虽然 LSTM/GRU 缓解了长距离依赖，但仍不如 Transformer 的 “自注意力”（能直接关注序列中任意位置的词，比如第 1 个和第 100 个词直接建立联系）。
  • Transformer 可并行计算（所有词同时处理），训练速度远快于 RNN 系列（按顺序处理）。

下午：动手实践（用 PyTorch 实现简单神经网络和 RNN）

1. 用 PyTorch 构建极简 MLP（多层感知器，基础神经网络）

（1）什么是 MLP？

• 最简单的神经网络，由 “输入层→隐藏层→输出层” 组成，用于处理简单分类问题（如 “判断数字是 0 还是 1”）。

（2）详细代码步骤（复制粘贴即可运行，每步附解释）

import torchimport torch.nn as nn # 神经网络模块import torch.optim as optim # 优化器（用于反向传播调整权重）# 步骤1：准备数据（二分类问题：输入2个数字，输出0或1）# 输入数据：4个样本，每个样本有2个特征X = torch.tensor([[0, 0], [0, 1], [1, 0], [1, 1]], dtype=torch.float32)# 标签（正确答案）：假设是“异或问题”（0^0=0, 0^1=1, 1^0=1, 1^1=0）y = torch.tensor([[0], [1], [1], [0]], dtype=torch.float32)# 步骤2：定义MLP模型（输入层2→隐藏层4→输出层1）class SimpleMLP(nn.Module): def __init__(self): super().__init__() self.layer1 = nn.Linear(2, 4) # 输入层→隐藏层（2特征→4神经元） self.activation = nn.ReLU() # 激活函数（给网络非线性能力） self.layer2 = nn.Linear(4, 1) # 隐藏层→输出层（4神经元→1输出） self.output_activation = nn.Sigmoid() # 输出压缩到0-1（表示概率） def forward(self, x): # 前向传播：输入→隐藏层→激活→输出层→输出激活 x = self.layer1(x) x = self.activation(x) x = self.layer2(x) x = self.output_activation(x) return x# 步骤3：初始化模型、损失函数、优化器model = SimpleMLP()criterion = nn.MSELoss() # 用均方误差损失（适合回归，这里简单分类也可用）optimizer = optim.SGD(model.parameters(), lr=0.1) # 随机梯度下降优化器# 步骤4：训练模型（反向传播更新权重）for epoch in range(1000): # 训练1000次 # 前向传播：计算预测结果 y_pred = model(X) # 计算损失（预测与真实的差距） loss = criterion(y_pred, y) # 反向传播： optimizer.zero_grad() # 清空上一次的梯度 loss.backward() # 计算梯度（损失对权重的导数） optimizer.step() # 更新权重（根据梯度调整） # 每100次打印一次损失（看是否下降） if (epoch + 1) % 100 == 0: print(f\"第{epoch+1}次训练，损失：{loss.item():.4f}\")# 步骤5：测试模型print(\"\\n预测结果（接近0为类别0，接近1为类别1）：\")with torch.no_grad(): # 不计算梯度（测试时无需更新） print(model(X))

• 预期输出：损失逐渐下降，最终预测结果接近[[0.], [1.], [1.], [0.]]，说明模型学会了 “异或” 规律。

2. 用 PyTorch 体验 LSTM（处理序列数据，如字符预测）

（1）任务：根据前一个字符预测下一个字符（简单序列任务）

• 例：输入 “h” 预测 “e”，输入 “e” 预测 “l”，最终能生成 “hello”。

（2）代码步骤（附详细注释）

import torchimport torch.nn as nnimport numpy as np# 步骤1：准备数据（简单字符序列）text = \"hello\"chars = list(set(text)) # 去重得到所有字符：[\'h\', \'e\', \'l\', \'o\']char_to_idx = {c: i for i, c in enumerate(chars)} # 字符→数字（如h→0, e→1）idx_to_char = {i: c for i, c in enumerate(chars)} # 数字→字符# 生成训练数据：输入前一个字符，输出后一个字符# 例：输入h(0)→输出e(1)；输入e(1)→输出l(2)；输入l(2)→输出l(2)；输入l(2)→输出o(3)inputs = [char_to_idx[c] for c in text[:-1]] # [0,1,2,2]targets = [char_to_idx[c] for c in text[1:]] # [1,2,2,3]# 转换为PyTorch张量（增加维度：[样本数, 序列长度, 特征数]，这里序列长度=1）inputs = torch.tensor(inputs).unsqueeze(1).long() # shape: (4,1)targets = torch.tensor(targets).long() # shape: (4,)# 步骤2：定义LSTM模型class SimpleLSTM(nn.Module): def __init__(self, input_size, hidden_size, output_size): super().__init__() self.hidden_size = hidden_size self.embedding = nn.Embedding(input_size, hidden_size) # 字符嵌入（把数字转为向量） self.lstm = nn.LSTM(hidden_size, hidden_size) # LSTM层 self.fc = nn.Linear(hidden_size, output_size) # 全连接层（输出预测） def forward(self, input, hidden): # 输入处理 embedded = self.embedding(input).view(1, 1, -1) # 调整形状 # LSTM前向传播 lstm_out, hidden = self.lstm(embedded, hidden) # 输出预测 output = self.fc(lstm_out.view(1, -1)) return output, hidden def init_hidden(self): # 初始化隐藏状态（初始记忆） return (torch.zeros(1, 1, self.hidden_size), torch.zeros(1, 1, self.hidden_size))# 步骤3：初始化模型、损失函数、优化器input_size = len(chars) # 输入大小=字符种类数（4）hidden_size = 16 # 隐藏层大小（可调整）output_size = len(chars) # 输出大小=字符种类数model = SimpleLSTM(input_size, hidden_size, output_size)criterion = nn.CrossEntropyLoss() # 交叉熵损失（适合分类，这里预测下一个字符）optimizer = optim.Adam(model.parameters(), lr=0.01)# 步骤4：训练LSTMfor epoch in range(1000): total_loss = 0 hidden = model.init_hidden() # 每次训练初始化隐藏状态 for i in range(len(inputs)): # 输入当前字符，目标是下一个字符 input_char = inputs[i:i+1] # 取一个字符 target_char = targets[i:i+1] # 前向传播 output, hidden = model(input_char, hidden) loss = criterion(output, target_char) # 反向传播 optimizer.zero_grad() loss.backward(retain_graph=True) # 保留计算图（因为hidden被复用） optimizer.step() total_loss += loss.item() # 每100次打印损失 if (epoch + 1) % 100 == 0: print(f\"第{epoch+1}次训练，平均损失：{total_loss/len(inputs):.4f}\")# 步骤5：测试LSTM生成字符print(\"\\n生成字符（从\'h\'开始）：\")hidden = model.init_hidden()input_char = torch.tensor([char_to_idx[\'h\']]) # 从\'h\'开始generated = [\'h\']for _ in range(4): # 生成4个字符（组成\"hello\"） output, hidden = model(input_char, hidden) # 取概率最大的字符作为预测 predicted_idx = torch.argmax(output).item() predicted_char = idx_to_char[predicted_idx] generated.append(predicted_char) input_char = torch.tensor([predicted_idx])print(\"生成结果：\", \'\'.join(generated)) # 理想输出：\"hello\"

• 预期输出：训练后损失下降，生成结果接近 “hello”（可能偶尔出错，因为数据太简单），体验 LSTM 处理序列的能力。

 总结：

1、神经网络：输入--前向传播--反向传播--更新权重

2、激活函数：RELU、Sigmoid、Tanh

3、损失函数：交叉熵损失函数用于分类问题、平方差函数用于回归问题

4、序列问题：自回归类型，与前面的输入有关

5、RNN:用于解决序列问题，用到前一时刻的输入信息，即Ht-1由Xt-1决定，Ht由Ht-1决定，但是只有短期记忆，存在长距离依赖问题

6、LSTM&GRU：引入门控机制，选择保留有用的信息，遗忘不重要的信息，缓解长距离依赖问题