2025年ASOC SCI2区TOP，无人机集群路径规划与任务分配的组合优化在多障碍战场环境中的应用，深度解析+性能实测

目录

• • 1.摘要
  • 2.数学模型
  • 3.改进RRT*-APF算法
  • 4.结果展示
  • 5.参考文献
  • 6.代码获取
  • 7. 算法辅导·应用定制·读者交流

1.摘要

为了提高无人机（UAV）的自主控制性能和综合作战能力，本文提出了一种用于无人机集群路径规划和任务分配的组合优化方法，涉及两个优化问题。对于路径规划，提出通过引入自适应势场调整和全局搜索，改进RRT*-APF算法。对比仿真结果表明，改进后的RRT*-APF算法在实现最短路径的同时，可以将优化时间减少超过80%。对于任务分配，输入最短路径后，采用考虑多重约束的离散粒子群算法（PSO）进行最优任务分配方案的求解。

2.数学模型

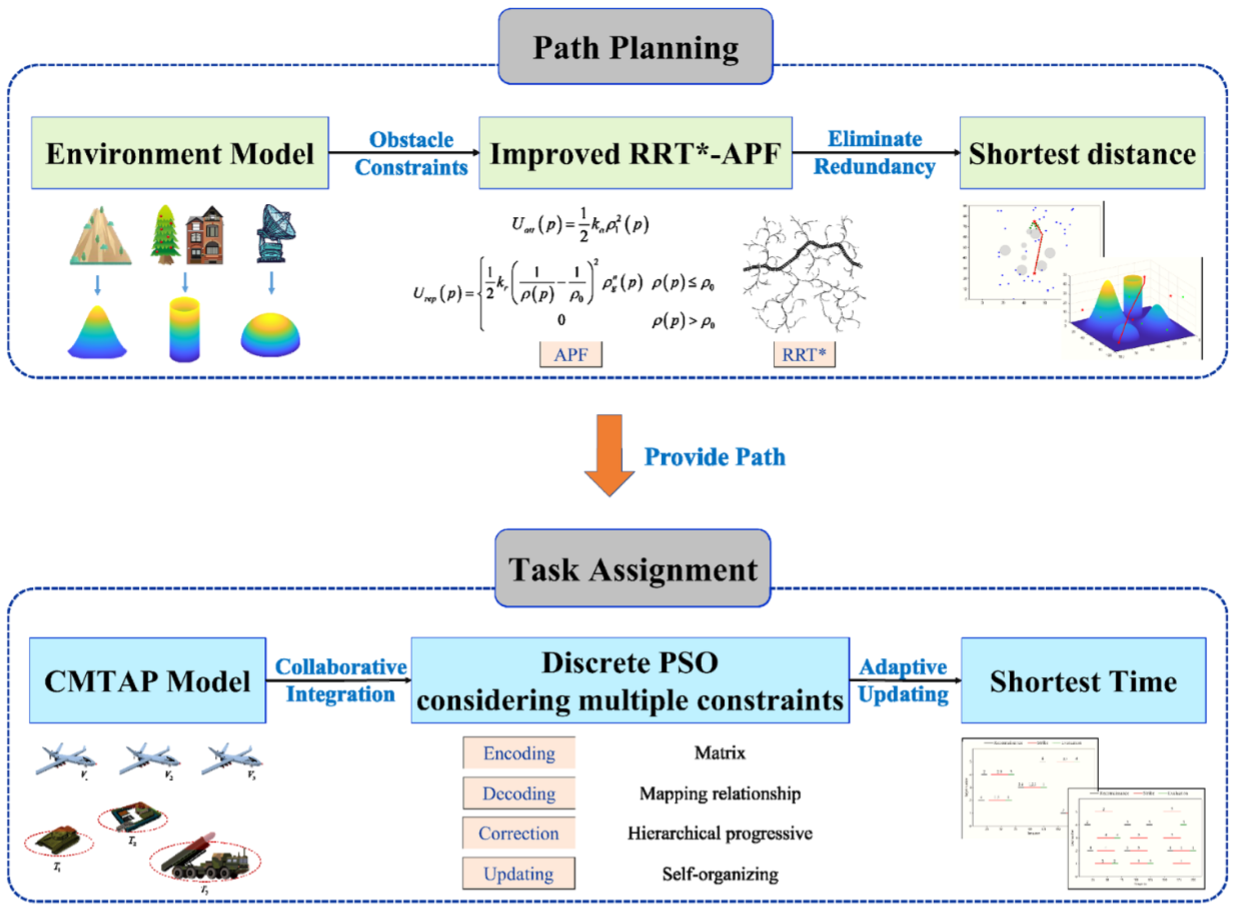
为了研究无人机路径规划，首先需要建立一个环境地图作为约束条件。环境地图中加入了障碍物，通常包括基地地形、障碍区域和威胁区域。

二维战场环境图

在二维战场环境中，采用圆形障碍物模型，障碍物区域定义为：
C i ( x , y ) = ( x − x i) 2 + ( y − y i) 2 ≤ r i 2 C_i(x,y)=(x-x_i)^2+(y-y_i)^2\\leq r_i^2 Ci​(x,y)=(x−xi​)2+(y−yi​)2≤ri2​

三维战场环境图

基地地形主要以山地地形为主，选取山顶函数模拟：
Z i( x , y ) = h ie x p[ − ( x − x o i a ) 2 − ( y − y o i b ) 2 ]( i = 1 , 2 , ⋯   , N M ) Z_i\\left(x,y\\right)=h_i\\mathrm{exp}\\left[-\\left(\\frac{x-x_{oi}}{a}\\right)^2-\\left(\\frac{y-y_{oi}}{b}\\right)^2\\right]\\left(i=1,2,\\cdots,N_M\\right) Zi​(x,y)=hi​exp[−(ax−xoi​​)2−(by−yoi​​)2](i=1,2,⋯,NM​)

适应度函数采用欧式距离度量。

论文采用协作多任务分配问题（CMTAP）模型，约束条件包括无人机类型和能力约束、任务时间顺序约束、任务时间约束、无人机协作约束。

3.改进RRT*-APF算法

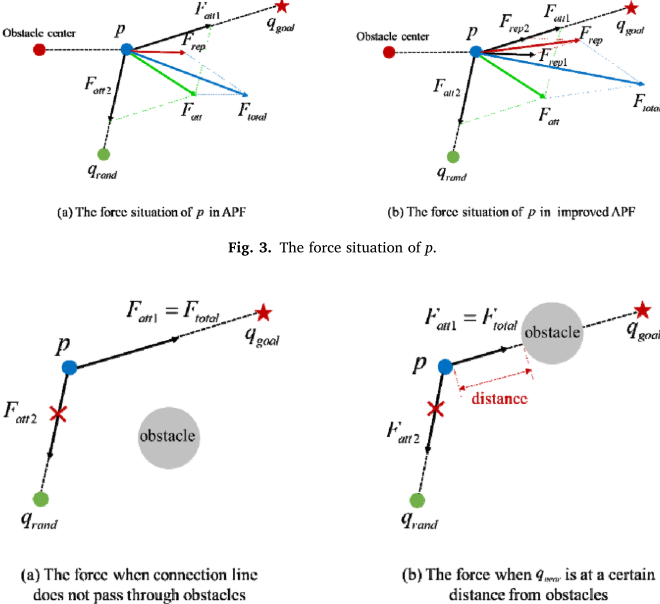
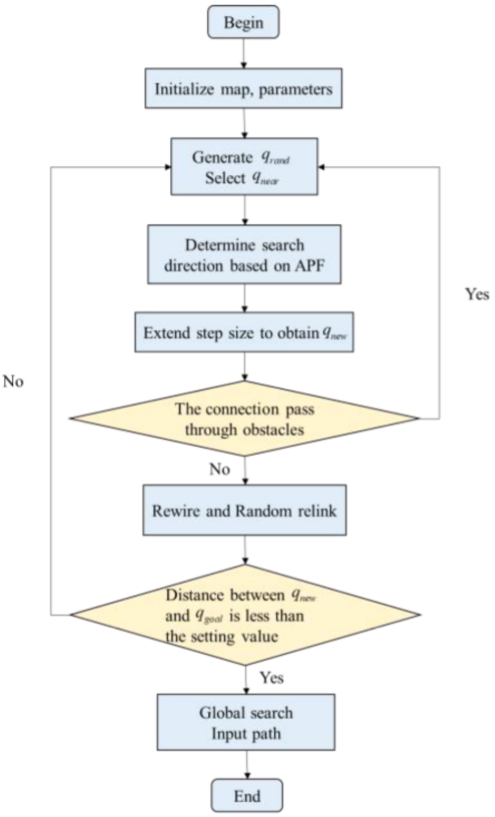
基于RRT* 算法，本文通过加入APF算法优化了 q n e w q_{new} qnew​的生成方法加快收敛速度。引入了自适应势场调整和全局搜索，进一步加速收敛速度并减少路径长度。

自适应势场调整

在生成 q n e w q_{new} qnew​时，如果 q n e a r q_{near} qnear​与 q g o a l q_{goal} qgoal​之间的连接不经过障碍物， q r a n d q_{rand} qrand​的吸引力可能会导致路径偏离最短路径。此时，移除 q r a n d q_{rand} qrand​的吸引势场，确保路径仅在 q g o a l q_{goal} qgoal​的吸引力作用下前进，从而沿直线到达 q g o a l q_{goal} qgoal​。当 q n e a r q_{near} qnear​与障碍物之间有一定距离时，也可以去除 q r a n d q_{rand} qrand​的吸引力，加速最短路径的搜索。

全局搜索

在优化过程中，由于新节点生成具有随机性，规划路径中可能出现多个转折点，因而需要进行全局优化。在全局优化过程中，判断路径中的任意两个节点之间的连接是否穿过障碍物。如果不穿过障碍物，则直接连接这两个节点。

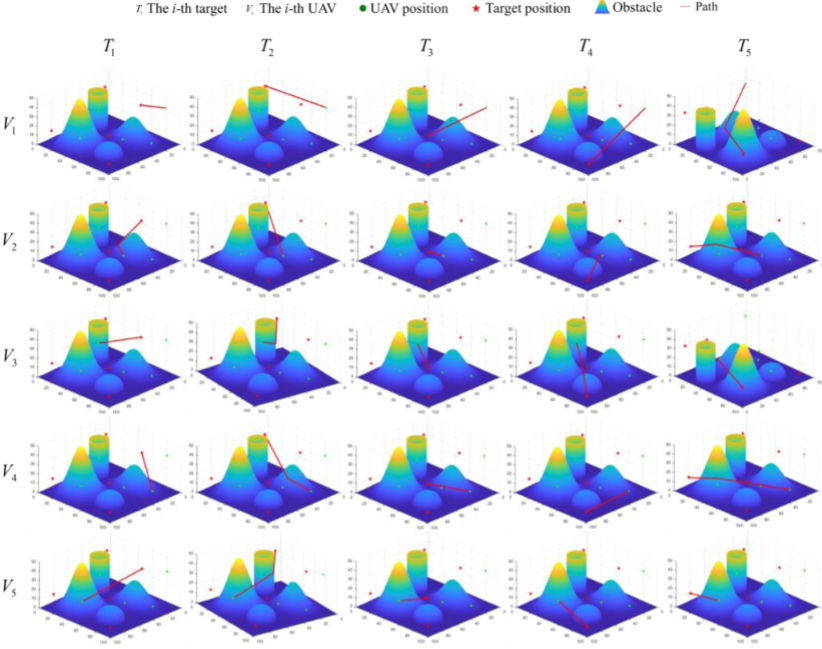
4.结果展示

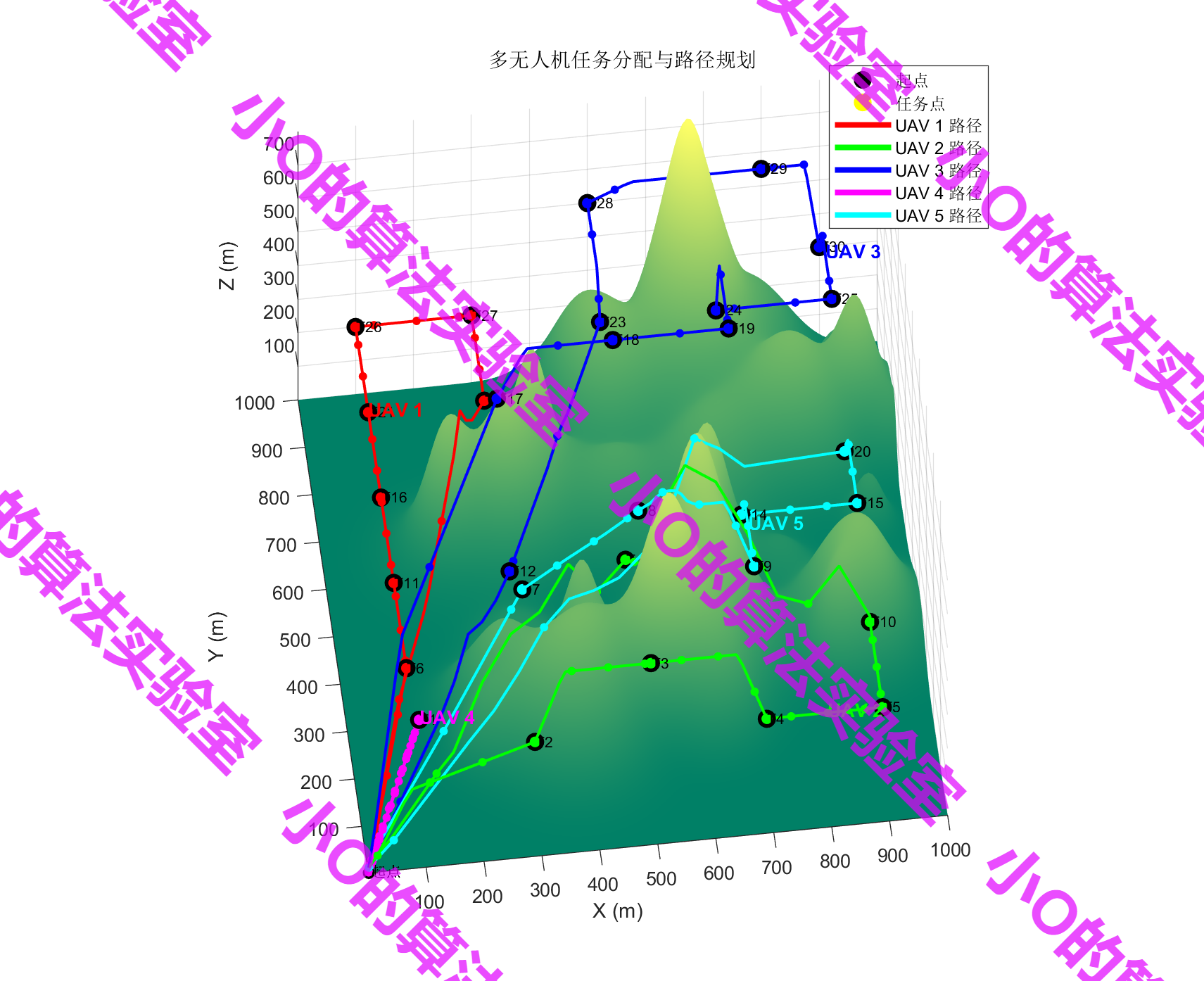
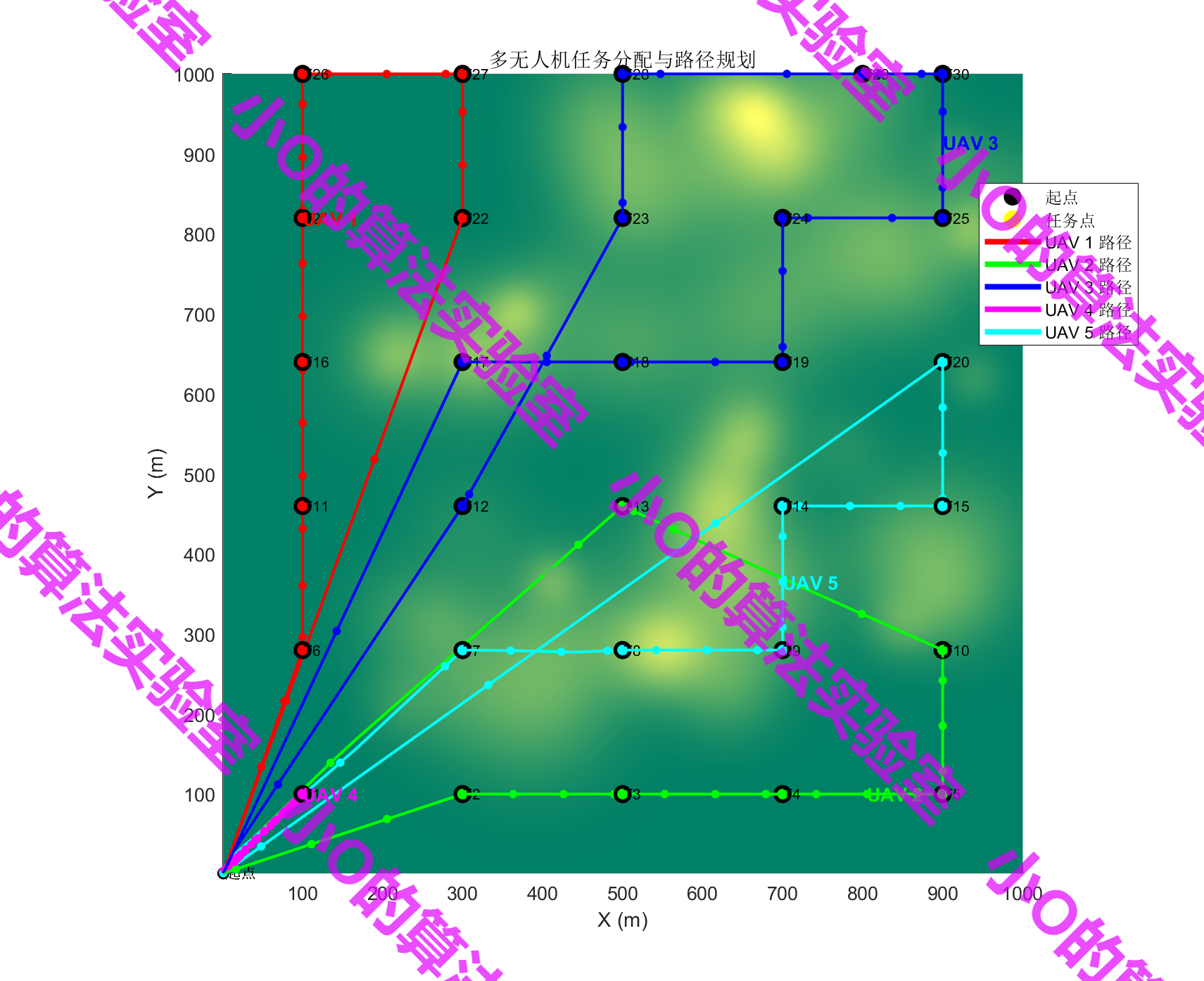
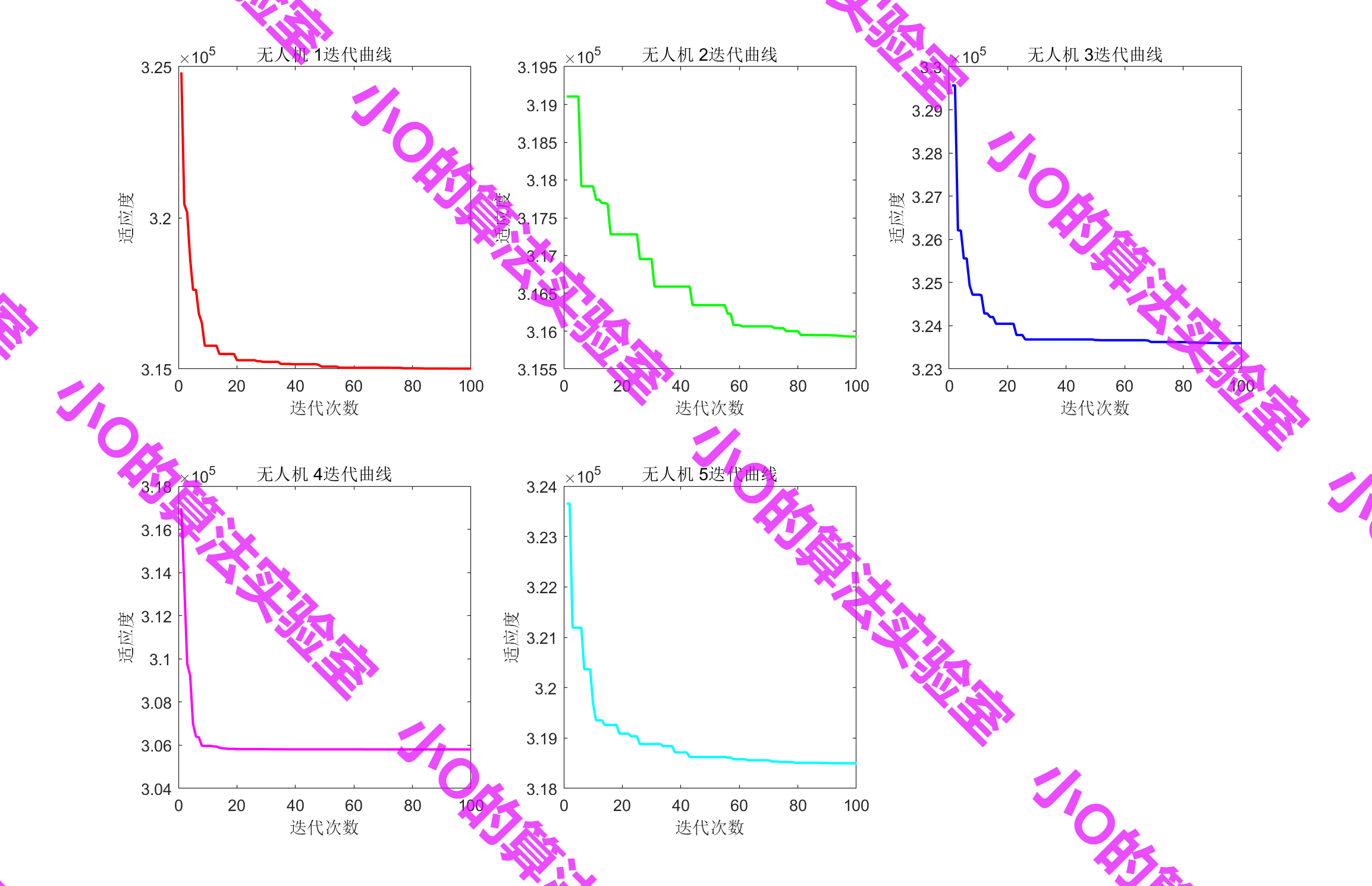
5.参考文献

[1] Guo C, Huang L, Tian K. Combinatorial optimization for UAV swarm path planning and task assignment in multi-obstacle battlefield environment[J]. Applied Soft Computing, 2025, 171: 112773.

6.代码获取

xx

7. 算法辅导·应用定制·读者交流