网站导航
> 技术文档 > 学习卡尔曼滤波（Kalman Filter）并在Stm32上验证_stm32 卡尔曼滤波

学习卡尔曼滤波（Kalman Filter）并在Stm32上验证_stm32 卡尔曼滤波

网友: 技术文档 2025-07-30 11:48:45

卡尔曼滤波（Kalman Filter）是一种强大的信号处理工具，广泛应用于噪声过滤和状态估计。本文将介绍卡尔曼滤波的使用场景和方法，并通过STM32F103的ADC采样实现，分别讲解一维、二维和三维卡尔曼滤波的代码和效果。

一、卡尔曼滤波的使用场景

卡尔曼滤波适用于从带噪声的测量数据中估计系统状态，特别适合以下场景：
    1.    传感器数据平滑：
    •    如ADC采集的电压、温度，或IMU的加速度、角速度，滤除噪声后得到更稳定的信号。
    2.    状态估计：
    •    机器人导航中，融合GPS和IMU数据估计位置和速度。
    •    自动驾驶中，跟踪车辆的运动轨迹。
    3.    预测与控制：
    •    电池管理系统（BMS）中，估计SOC（荷电状态）和SOH（健康状态）。
    •    工业控制中，实时校正传感器偏差。
在嵌入式系统中，卡尔曼滤波因计算效率高、递归性强，非常适合单片机实现。

二、卡尔曼滤波的使用方法

卡尔曼滤波的核心是预测和更新两个步骤，基于线性系统和高斯噪声假设。以下是通用流程：
    1.    系统建模：
    •    定义状态向量（如位置、速度）。
    •    建立状态转移模型（描述状态如何随时间变化）。
    •    定义测量模型（传感器如何观测状态）。
    2.    初始化：
    •    设置初始状态估计、估计协方差、过程噪声协方差（Q）、测量噪声协方差（R）。
    3.    预测：
    •    根据状态转移方程预测下一时刻状态。
    •    更新估计协方差。
    4.    更新：
    •    计算卡尔曼增益（权衡预测和测量）。
    •    结合实际测量值修正状态估计。
    •    更新协方差。
数学公式（以一维为例）：
    •    预测：  \\hat{x}_{k|k-1} = \\hat{x}_{k-1|k-1}, \\quad P_{k|k-1} = P_{k-1|k-1} + Q 
    •    更新： 

        ​​​​​​ K_k = \\frac{P_{k|k-1}}{P_{k|k-1} + R}, \\quad \\hat{x}_{k|k} = \\hat{x}_{k|k-1} + K_k (z_k - \\hat{x}_{k|k-1}), \\quad P_{k|k} = (1 - K_k) P_{k|k-1}  

        其中：
    •    \\hat{x}: 状态估计
    •    P: 估计协方差
    •    Q: 过程噪声协方差
    •    R: 测量噪声协方差
    •    K: 卡尔曼增益
    •    z_k: 测量值

再详细点就是
    1.    状态预测：
    •    状态估计： \\hat{x}_{k|k-1} = \\hat{x}_{k-1|k-1} （假设状态不随时间变化，或有简单的动态模型）。
    •    协方差预测：P_{k|k-1} = P_{k-1|k-1} + Q，其中 ( Q ) 是过程噪声协方差。
    2.    测量更新：
    •    卡尔曼增益：K_k = \\frac{P_{k|k-1}}{P_{k|k-1} + R} ，其中 ( R ) 是测量噪声协方差。
    •    状态更新： \\hat{x}_{k|k} = \\hat{x}_{k|k-1} + K_k (z_k - \\hat{x}_{k|k-1}) ，其中 ( z_k ) 是ADC测量值。
    •    协方差更新： P_{k|k} = (1 - K_k) P_{k|k-1} 。
关键参数：
    •    \\hat{x}：估计值（滤波后的ADC值）。
    •    P：估计误差协方差，反映估计的不确定性。
    •    Q：过程噪声（系统本身的随机变化，通常较小）。
    •    R：测量噪声（噪声，需根据实际测量估计）。

三、STM32F103 ADC采样实践

我们以STM32F103（Cortex-M3，带12位ADC）为例，通过ADC采集模拟电压信号，分别实现一维、二维和三维卡尔曼滤波。硬件假设：
    •    使用PA0（ADC1通道0）采集0-3.3V电压。
    •    目标：滤除ADC噪声，得到平滑信号。

3.1 ADC 配置

使用STM32CubeMX配置ADC在这里就不多说了，读取adc转换的值为如下代码。当然也可以直接对adc_value进行滤波。代码基于HAL库：

float Read_ADC(void) { HAL_ADC_Start(&hadc1); HAL_ADC_PollForConversion(&hadc1, HAL_MAX_DELAY); uint16_t adc_value = HAL_ADC_GetValue(&hadc1); return (float)adc_value * 3.3f / 4095.0f; // 转换为电压}

3.2 一维卡尔曼滤波

直接平滑ADC采集的电压值，假设电压变化缓慢（无明显动态）。
模型
    •    状态：电压值  x。
    •    状态转移： x_k = x_{k-1} （静态系统）。
    •    测量： z_k = x_k + v_k ，其中 v_k 是ADC噪声。

代码如下：

typedef struct { float x; // 状态估计（电压） float P; // 估计协方差 float Q; // 过程噪声协方差 float R; // 测量噪声协方差} Kalman1D;void Kalman1D_Init(Kalman1D *kf, float initial_x, float initial_P, float Q, float R) { kf->x = initial_x; kf->P = initial_P; kf->Q = Q; kf->R = R;}float Kalman1D_Update(Kalman1D *kf, float measurement) { // 预测 kf->P = kf->P + kf->Q; // 更新 float K = kf->P / (kf->P + kf->R); kf->x = kf->x + K * (measurement - kf->x); kf->P = (1 - K) * kf->P; return kf->x;}Kalman1D kf;int main(void) { HAL_Init(); /*中间初始化代码*/ Kalman1D_Init(&kf, 0.0f, 1.0f, 0.001f, 0.1f); // Q=0.001, R=0.1 while (1) { float voltage = Read_ADC(); float filtered_voltage = Kalman1D_Update(&kf, voltage); printf(\"Raw: %.3f V, Filtered: %.3f V\\n\", voltage, filtered_voltage); HAL_Delay(10); }}

参数说明
    •    R：通过采集静止信号，计算ADC电压方差（比如0.1）。
    •    Q：设为小值（如0.001），因为电压变化慢。
    •    效果：假设输入1.5V带噪声信号（1.4-1.6V抖动），滤波后稳定在1.5V左右。

3.3 二维卡尔曼滤波

假设电压有缓慢变化趋势（如传感器漂移），我们跟踪电压和其变化率（类似速度）。
模型
    •    状态： \\mathbf{x} = [x, \\dot{x}]^T ，其中  x 是电压， \\dot{x}  是电压变化率。
    •    状态转移： \\mathbf{x}k = \\begin{bmatrix} 1 & \\Delta t \\\\ 0 & 1 \\end{bmatrix} \\mathbf{x}_{k-1} +\\mathbf{w}_k  其中 \\Delta t 是采样间隔（如0.01s）。
    •    测量：z_k = [1, 0] \\mathbf{x}_k + v_k （仅测量电压）。

代码实现:

#include  // 使用ARM CMSIS库进行矩阵运算typedef struct { float x[2]; // 状态 [电压, 变化率] float P[2][2]; // 协方差矩阵 float Q[2][2]; // 过程噪声协方差 float R; // 测量噪声协方差 float dt; // 采样间隔} Kalman2D;void Kalman2D_Init(Kalman2D *kf, float initial_x, float initial_dx, float dt) { kf->x[0] = initial_x; kf->x[1] = initial_dx; kf->P[0][0] = 1.0f; kf->P[0][1] = 0.0f; kf->P[1][0] = 0.0f; kf->P[1][1] = 1.0f; kf->Q[0][0] = 0.001f; kf->Q[0][1] = 0.0f; kf->Q[1][0] = 0.0f; kf->Q[1][1] = 0.001f; kf->R = 0.1f; kf->dt = dt;}float Kalman2D_Update(Kalman2D *kf, float measurement) { // 状态转移矩阵 float A[2][2] = {{1, kf->dt}, {0, 1}}; float H[2] = {1, 0}; // 测量矩阵 // 预测 float x_pred[2]; x_pred[0] = A[0][0] * kf->x[0] + A[0][1] * kf->x[1]; x_pred[1] = A[1][0] * kf->x[0] + A[1][1] * kf->x[1]; float P_pred[2][2]; P_pred[0][0] = A[0][0] * (kf->P[0][0] * A[0][0] + kf->P[0][1] * A[1][0]) +  A[0][1] * (kf->P[1][0] * A[0][0] + kf->P[1][1] * A[1][0]) + kf->Q[0][0]; // 类似计算其他元素... // 更新 float innovation = measurement - (H[0] * x_pred[0] + H[1] * x_pred[1]); float S = H[0] * (P_pred[0][0] * H[0] + P_pred[0][1] * H[1]) +  H[1] * (P_pred[1][0] * H[0] + P_pred[1][1] * H[1]) + kf->R; float K[2]; K[0] = (P_pred[0][0] * H[0] + P_pred[0][1] * H[1]) / S; K[1] = (P_pred[1][0] * H[0] + P_pred[1][1] * H[1]) / S; kf->x[0] = x_pred[0] + K[0] * innovation; kf->x[1] = x_pred[1] + K[1] * innovation; // 更新协方差（简化） kf->P[0][0] = (1 - K[0] * H[0]) * P_pred[0][0]; // 类似更新其他元素... return kf->x[0];}/************** 主程序*************/Kalman2D kf;int main(void) { HAL_Init(); ADC_Init(); Kalman2D_Init(&kf, 0.0f, 0.0f, 0.01f); while (1) { float voltage = Read_ADC(); float filtered_voltage = Kalman2D_Update(&kf, voltage); printf(\"Raw: %.3f V, Filtered: %.3f V\\n\", voltage, filtered_voltage); HAL_Delay(10); }}

参数与效果
    •    R, Q：类似一维，Q可稍大（如0.01）以适应变化率。
    •    效果：能跟踪缓慢变化的电压（如线性漂移），比一维更平滑

3.4 三维卡尔曼滤波

假设电压有更复杂的动态（如加速度模型），跟踪电压、变化率和加速度。
模型
    •    状态： \\mathbf{x} = [x, \\dot{x}, \\ddot{x}]^T。表示电压，变化率，加速度。
    •    状态转移：  \\mathbf{x}k = \\begin{bmatrix} 1 & \\Delta t & \\frac{\\Delta t^2}{2} \\\\ 0 & 1 & \\Delta t \\\\ 0 & 0 & 1 \\end{bmatrix} \\mathbf{x}_{k-1} + \\mathbf{w}_k 

\\mathbf{w}_k是过程噪声，协方差矩阵为Q。
    •    测量：z_k = [1, 0, 0] \\mathbf{x}_k + v_k 。

因为ADC只是测量电压，v_k是测量噪声，协方差为R

噪声参数说明：

Q：过程噪声协方差，设为对角矩阵，反映状态变化的不确定性。

R：测量噪声协方差，通过实验估计ADC噪声

代码实现：

共有两种一种不使用CMSIS-DSP库，简单的矩阵运算另一种使用CMSIS-DSP库

不使用CMSIS-DSP库：

#include \"stm32f1xx_hal.h\"#include // 三维卡尔曼滤波器结构体typedef struct { float x[3]; // 状态向量 [电压, 变化率, 加速度] float P[3][3]; // 估计协方差矩阵 float Q[3][3]; // 过程噪声协方差矩阵 float R;  // 测量噪声协方差 float dt; // 采样间隔（秒）} Kalman3D;// 初始化三维卡尔曼滤波器void Kalman3D_Init(Kalman3D *kf, float initial_x, float initial_dx, float initial_ddx, float dt) { // 初始状态 kf->x[0] = initial_x; // 初始电压 kf->x[1] = initial_dx; // 初始变化率 kf->x[2] = initial_ddx; // 初始加速度 // 初始协方差矩阵（单位矩阵，表示初始不确定性） for (int i = 0; i < 3; i++) { for (int j = 0; j P[i][j] = (i == j) ? 1.0f : 0.0f; } } // 过程噪声协方差（对角矩阵，假设各状态独立） for (int i = 0; i < 3; i++) { for (int j = 0; j Q[i][j] = (i == j) ? 0.001f : 0.0f; } } // 测量噪声协方差（通过实验估计） kf->R = 0.1f; // 采样间隔 kf->dt = dt;}// 三维卡尔曼滤波更新float Kalman3D_Update(Kalman3D *kf, float measurement) { // 状态转移矩阵 A float A[3][3] = { {1.0f, kf->dt, 0.5f * kf->dt * kf->dt}, {0.0f, 1.0f, kf->dt}, {0.0f, 0.0f, 1.0f} }; // 测量矩阵 H float H[3] = {1.0f, 0.0f, 0.0f}; // 临时变量 float x_pred[3]; // 预测状态 float P_pred[3][3]; // 预测协方差 float K[3]; // 卡尔曼增益 // 1. 预测步骤 // 状态预测：x_pred = A * x for (int i = 0; i < 3; i++) { x_pred[i] = 0.0f; for (int j = 0; j x[j]; } } // 协方差预测：P_pred = A * P * A^T + Q float temp[3][3] = {0}; // temp = A * P for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) { for (int k = 0; k P[k][j]; } } } // P_pred = temp * A^T + Q for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) { P_pred[i][j] = 0.0f; for (int k = 0; k Q[i][j]; } } // 2. 更新步骤 // 创新（测量残差）：y = z - H * x_pred float y = measurement - (H[0] * x_pred[0] + H[1] * x_pred[1] + H[2] * x_pred[2]); // 创新协方差：S = H * P_pred * H^T + R float S = 0.0f; float temp_H[3] = {0}; // temp_H = P_pred * H^T for (int i = 0; i < 3; i++) { for (int j = 0; j R; // 卡尔曼增益：K = P_pred * H^T / S for (int i = 0; i < 3; i++) { K[i] = temp_H[i] / S; } // 状态更新：x = x_pred + K * y for (int i = 0; i x[i] = x_pred[i] + K[i] * y; } // 协方差更新：P = (I - K * H) * P_pred float I_KH[3][3] = {0}; for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) { I_KH[i][j] = (i == j ? 1.0f : 0.0f) - K[i] * H[j]; } } // P = I_KH * P_pred for (int i = 0; i < 3; i++) { for (int j = 0; j P[i][j] = 0.0f; for (int k = 0; k P[i][j] += I_KH[i][k] * P_pred[k][j]; } } } return kf->x[0]; // 返回滤波后的电压}// 主程序Kalman3D kf;int main(void) { HAL_Init(); ADC_Init(); // 初始化三维卡尔曼滤波器 Kalman3D_Init(&kf, 0.0f, 0.0f, 0.0f, 0.01f); // 初始电压=0, dt=0.01s while (1) { // 读取 ADC float voltage = Read_ADC(); // 卡尔曼滤波 float filtered_voltage = Kalman3D_Update(&kf, voltage); // 输出结果（通过串口） printf(\"Raw: %.3f V, Filtered: %.3f V\\n\", voltage, filtered_voltage); HAL_Delay(10); // 每10ms采样一次 }}

带CMSIS-DSP

使用arm的CMSIS_DSP库，适用于高频或多维使用

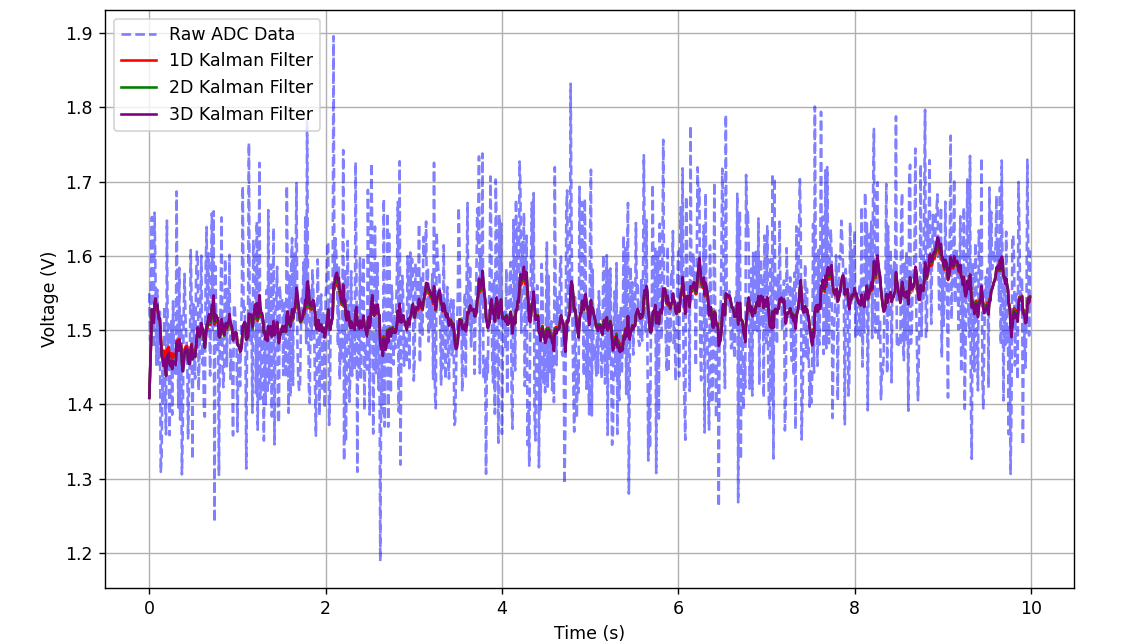
#include \"stm32f1xx_hal.h\"#include \"arm_math.h\"#include // ADC 句柄（需在 STM32CubeMX 中配置）extern ADC_HandleTypeDef hadc1;// 三维卡尔曼滤波器结构体typedef struct { arm_matrix_instance_f32 x; // 状态向量 [电压, 变化率, 加速度] (3x1) arm_matrix_instance_f32 P; // 估计协方差矩阵 (3x3) arm_matrix_instance_f32 Q; // 过程噪声协方差矩阵 (3x3) float R;  // 测量噪声协方差 float dt;  // 采样间隔（秒） // 辅助矩阵（预分配，避免动态分配） arm_matrix_instance_f32 A; // 状态转移矩阵 (3x3) arm_matrix_instance_f32 H; // 测量矩阵 (1x3) arm_matrix_instance_f32 x_pred; // 预测状态 (3x1) arm_matrix_instance_f32 P_pred; // 预测协方差 (3x3) arm_matrix_instance_f32 K; // 卡尔曼增益 (3x1)} Kalman3D;// 矩阵数据存储float x_data[3]; // 状态向量float P_data[9]; // 协方差矩阵 (3x3)float Q_data[9]; // 过程噪声协方差float A_data[9]; // 状态转移矩阵float H_data[3]; // 测量矩阵float x_pred_data[3]; // 预测状态float P_pred_data[9]; // 预测协方差float K_data[3]; // 卡尔曼增益// 初始化三维卡尔曼滤波器void Kalman3D_Init(Kalman3D *kf, float initial_x, float initial_dx, float initial_ddx, float dt) { // 初始化状态向量 x x_data[0] = initial_x; x_data[1] = initial_dx; x_data[2] = initial_ddx; arm_mat_init_f32(&kf->x, 3, 1, x_data); // 初始化协方差矩阵 P (单位矩阵) for (int i = 0; i P, 3, 3, P_data); // 初始化过程噪声协方差 Q (对角矩阵) for (int i = 0; i Q, 3, 3, Q_data); // 初始化状态转移矩阵 A A_data[0] = 1.0f; A_data[1] = dt; A_data[2] = 0.5f * dt * dt; A_data[3] = 0.0f; A_data[4] = 1.0f; A_data[5] = dt; A_data[6] = 0.0f; A_data[7] = 0.0f; A_data[8] = 1.0f; arm_mat_init_f32(&kf->A, 3, 3, A_data); // 初始化测量矩阵 H H_data[0] = 1.0f; H_data[1] = 0.0f; H_data[2] = 0.0f; arm_mat_init_f32(&kf->H, 1, 3, H_data); // 初始化预测状态和协方差 arm_mat_init_f32(&kf->x_pred, 3, 1, x_pred_data); arm_mat_init_f32(&kf->P_pred, 3, 3, P_pred_data); // 初始化卡尔曼增益 arm_mat_init_f32(&kf->K, 3, 1, K_data); // 测量噪声协方差 kf->R = 0.1f; // 采样间隔 kf->dt = dt;}// 三维卡尔曼滤波更新float Kalman3D_Update(Kalman3D *kf, float measurement) { // 临时矩阵 float temp1_data[9]; // 3x3 float temp2_data[3]; // 3x1 float temp3_data[1]; // 1x1 arm_matrix_instance_f32 temp1, temp2, temp3; arm_mat_init_f32(&temp1, 3, 3, temp1_data); arm_mat_init_f32(&temp2, 3, 1, temp2_data); arm_mat_init_f32(&temp3, 1, 1, temp3_data); // 1. 预测步骤 // 状态预测：x_pred = A * x arm_mat_mult_f32(&kf->A, &kf->x, &kf->x_pred); // 协方差预测：P_pred = A * P * A^T + Q arm_mat_mult_f32(&kf->A, &kf->P, &temp1); // temp1 = A * P arm_mat_trans_f32(&kf->A, &temp1); // temp1 = A^T (复用 temp1) arm_mat_mult_f32(&temp1, &kf->A, &kf->P_pred); // P_pred = (A * P) * A^T arm_mat_add_f32(&kf->P_pred, &kf->Q, &kf->P_pred); // P_pred += Q // 2. 更新步骤 // 创新：y = z - H * x_pred arm_mat_mult_f32(&kf->H, &kf->x_pred, &temp3); // temp3 = H * x_pred float y = measurement - temp3_data[0]; // 创新协方差：S = H * P_pred * H^T + R arm_mat_mult_f32(&kf->H, &kf->P_pred, &temp2); // temp2 = H * P_pred arm_mat_trans_f32(&kf->H, &temp1); // temp1 = H^T arm_mat_mult_f32(&temp2, &temp1, &temp3); // temp3 = (H * P_pred) * H^T float S = temp3_data[0] + kf->R; // 卡尔曼增益：K = P_pred * H^T / S arm_mat_trans_f32(&kf->H, &temp1); // temp1 = H^T arm_mat_mult_f32(&kf->P_pred, &temp1, &kf->K); // K = P_pred * H^T arm_mat_scale_f32(&kf->K, 1.0f / S, &kf->K); // K /= S // 状态更新：x = x_pred + K * y arm_mat_scale_f32(&kf->K, y, &temp2); // temp2 = K * y arm_mat_add_f32(&kf->x_pred, &temp2, &kf->x); // x = x_pred + K * y // 协方差更新：P = (I - K * H) * P_pred arm_mat_mult_f32(&kf->K, &kf->H, &temp1); // temp1 = K * H arm_mat_scale_f32(&temp1, -1.0f, &temp1); // temp1 = -K * H for (int i = 0; i P_pred, &kf->P); // P = (I - K * H) * P_pred return kf->x.pData[0]; // 返回滤波后的电压}// 主程序Kalman3D kf;int main(void) { HAL_Init(); ADC_Init(); // 初始化三维卡尔曼滤波器 Kalman3D_Init(&kf, 0.0f, 0.0f, 0.0f, 0.01f); // 初始电压=0, dt=0.01s while (1) { // 读取 ADC float voltage = Read_ADC(); // 卡尔曼滤波 float filtered_voltage = Kalman3D_Update(&kf, voltage); // 输出结果（通过串口） printf(\"Raw: %.3f V, Filtered: %.3f V\\n\", voltage, filtered_voltage); HAL_Delay(10); // 每10ms采样一次 }}

python模拟效果，参数一样时： 

四、总结与调试

    参数调优：
    •    R：通过实验测量ADC噪声方差。
    •    Q：从小值开始，逐渐调整以平衡平滑度和响应速度。
通过一维到三维的实现，我们看到卡尔曼滤波的灵活性：
    •    一维：简单高效，适合静态信号。
    •    二维：能跟踪趋势，适合缓慢变化。
    •    三维：适合复杂动态，需权衡计算成本。
希望这篇文章对你的嵌入式学习有帮助！未来可以尝试融合多传感器数据（如IMU+GPS），体验卡尔曼滤波的更多魅力。 

网络标签：

相关问题